A Functional Extension of Semi-Structured Networks

Semi-structured networks (SSNs) merge the structures familiar from additive models with deep neural networks, allowing the modeling of interpretable partial feature effects while capturing higher-order non-linearities at the same time. A significant challenge in this integration is maintaining the interpretability of the additive model component. Inspired by large-scale biomechanics datasets, this paper explores extending SSNs to functional data. Existing methods in functional data analysis are promising but often not expressive enough to account for all interactions and non-linearities and do not scale well to large datasets. Although the SSN approach presents a compelling potential solution, its adaptation to functional data remains complex. In this work, we propose a functional SSN method that retains the advantageous properties of classical functional regression approaches while also improving scalability. Our numerical experiments demonstrate that this approach accurately recovers underlying signals, enhances predictive performance, and performs favorably compared to competing methods.

Functional additive regression on shape and form manifolds of planar curves

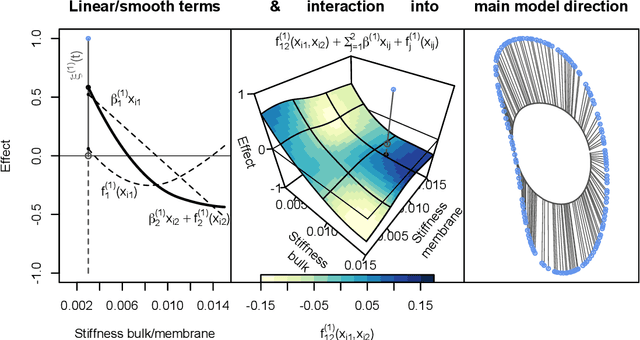
Defining shape and form as equivalence classes under translation, rotation and -- for shapes -- also scale, we extend generalized additive regression to models for the shape/form of planar curves or landmark configurations. The model respects the resulting quotient geometry of the response, employing the squared geodesic distance as loss function and a geodesic response function mapping the additive predictor to the shape/form space. For fitting the model, we propose a Riemannian $L_2$-Boosting algorithm well-suited for a potentially large number of possibly parameter-intensive model terms, which also yiels automated model selection. We provide novel intuitively interpretable visualizations for (even non-linear) covariate effects in the shape/form space via suitable tensor based factorizations. The usefulness of the proposed framework is illustrated in an analysis of 1) astragalus shapes of wild and domesticated sheep and 2) cell forms generated in a biophysical model, as well as 3) in a realistic simulation study with response shapes and forms motivated from a dataset on bottle outlines.