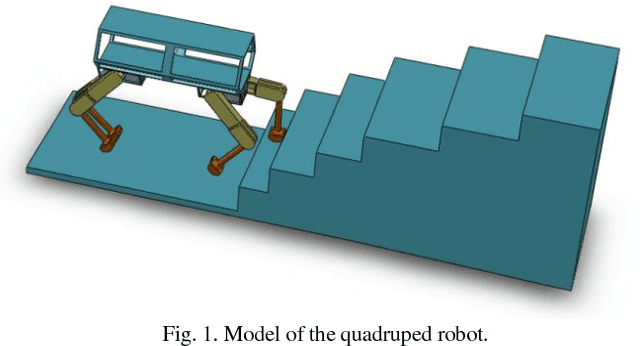
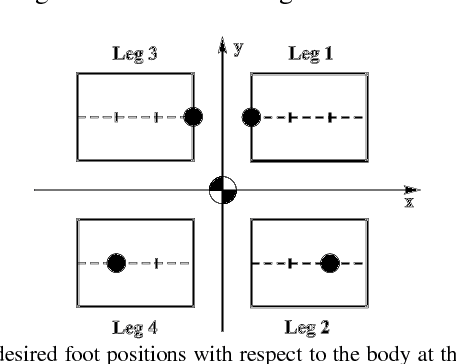
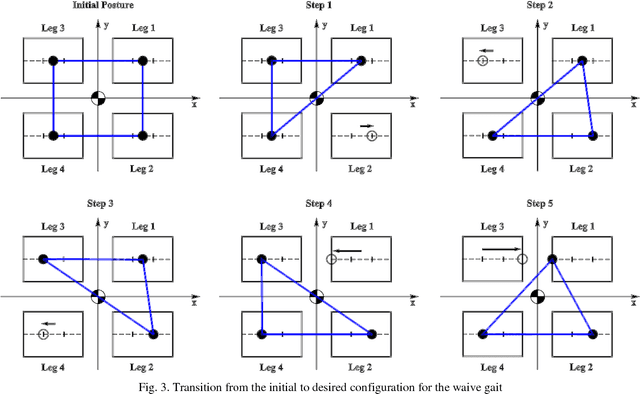
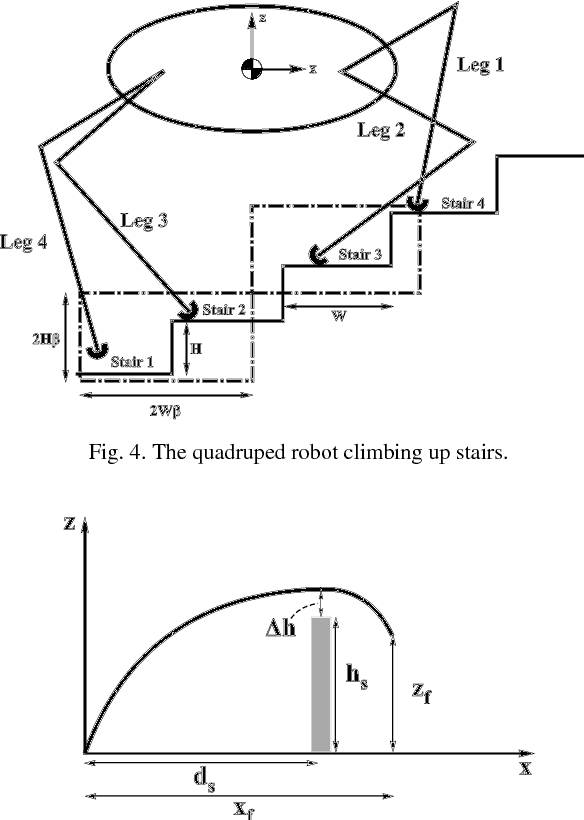
Stable Stair-Climbing of a Quadruped Robot

Synthesizing a stable gait that enables a quadruped robot to climb stairs is the focus of this paper. To this end, first a stable transition from initial to desired configuration is made based on the minimum number of steps and maximum use of the leg workspace to prepare the robot for the movement. Next, swing leg and body trajectories are planned for a successful stair- climbing gait. Afterwards, a stable spinning gait is proposed to change the orientation of the body. We simulate our gait planning algorithms on a model of quadruped robot. The results show that the robot is able to climb up stairs, rotate about its yaw axis, and climb down stairs while its stability is guaranteed.

Switching between Limit Cycles in a Model of Running Using Exponentially Stabilizing Discrete Control Lyapunov Function

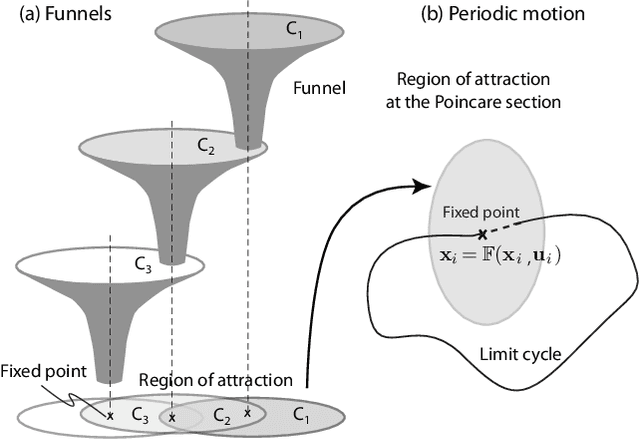
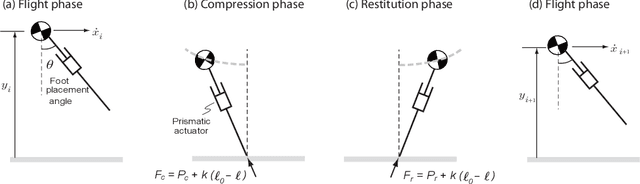
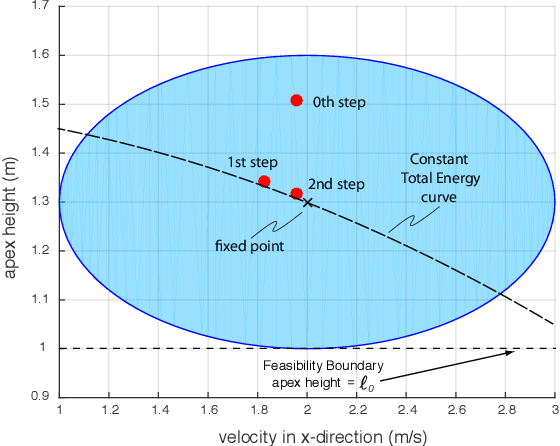
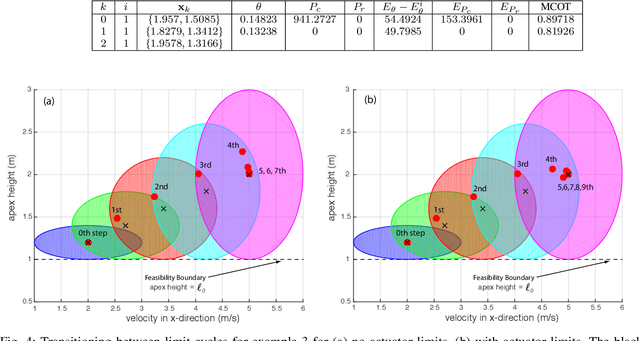
This paper considers the problem of switching between two periodic motions, also known as limit cycles, to create agile running motions. For each limit cycle, we use a control Lyapunov function to estimate the region of attraction at the apex of the flight phase. We switch controllers at the apex, only if the current state of the robot is within the region of attraction of the subsequent limit cycle. If the intersection between two limit cycles is the null set, then we construct additional limit cycles till we are able to achieve sufficient overlap of the region of attraction between sequential limit cycles. Additionally, we impose an exponential convergence condition on the control Lyapunov function that allows us to rapidly transition between limit cycles. Using the approach we demonstrate switching between 5 limit cycles in about 5 steps with the speed changing from 2 m/s to 5 m/s.