FR3D: Three-dimensional Flow Reconstruction and Force Estimation for Unsteady Flows Around Arbitrary Bluff Bodies via Conformal Mapping Aided Convolutional Autoencoders

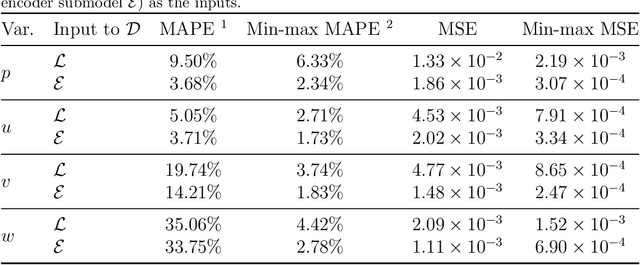
In many practical fluid dynamics experiments, measuring variables such as velocity and pressure is possible only at a limited number of sensor locations, or for a few two-dimensional planes in the flow. However, knowledge of the full fields is necessary to understand the dynamics of many flows. Deep learning reconstruction of full flow fields from sparse measurements has recently garnered significant research interest, as a way of overcoming this limitation. This task is referred to as the flow reconstruction (FR) task. In the present study, we propose a convolutional autoencoder based neural network model, dubbed FR3D, which enables FR to be carried out for three-dimensional flows around extruded 3D objects with arbitrary cross-sections. An innovative mapping approach, whereby multiple fluid domains are mapped to an annulus, enables FR3D to generalize its performance to objects not encountered during training. We conclusively demonstrate this generalization capability using a dataset composed of 80 training and 20 testing geometries, all randomly generated. We show that the FR3D model reconstructs pressure and velocity components with a few percentage points of error. Additionally, using these predictions, we accurately estimate the Q-criterion fields as well lift and drag forces on the geometries.

Deep learning fluid flow reconstruction around arbitrary two-dimensional objects from sparse sensors using conformal mappings

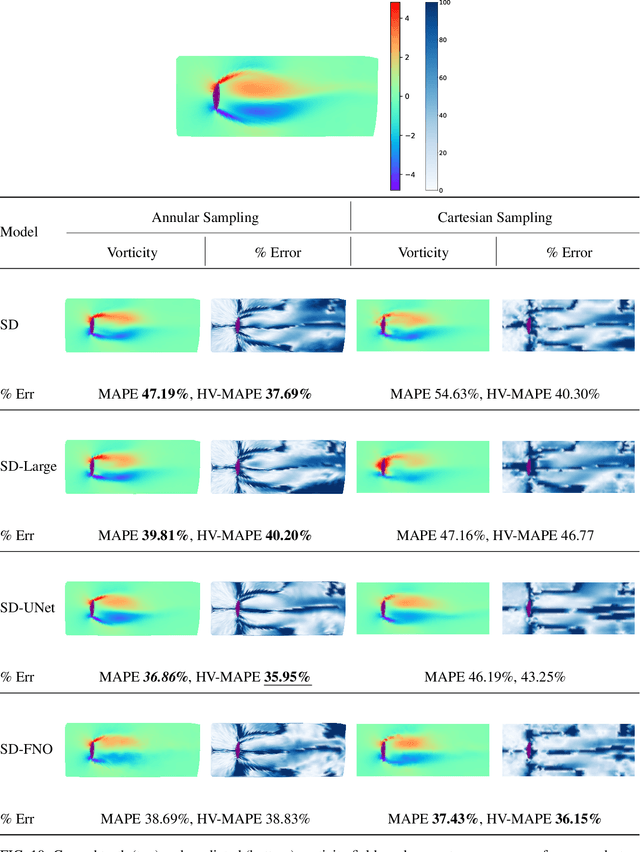
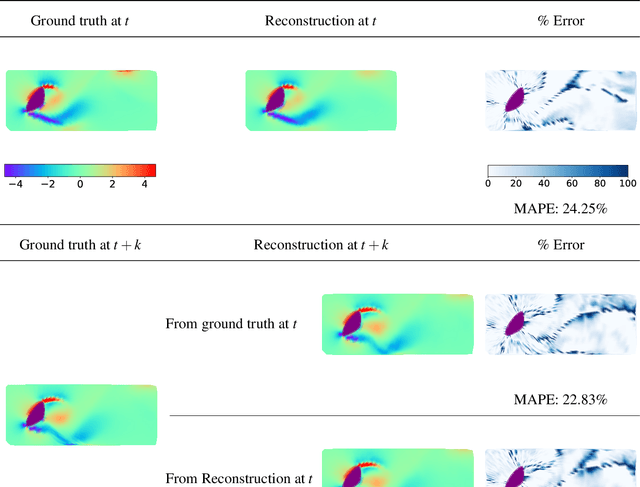
The usage of deep neural networks (DNNs) for flow reconstruction (FR) tasks from a limited number of sensors is attracting strong research interest, owing to DNNs' ability to replicate very high dimensional relationships. Trained over a single flow case for a given Reynolds number or over a reduced range of Reynolds numbers, these models are unfortunately not able to handle fluid flows around different objects without re-training. In this work, we propose a new framework called Spatial Multi-Geometry FR (SMGFR) task, capable of reconstructing fluid flows around different two-dimensional objects without re-training, mapping the computational domain as an annulus. Different DNNs for different sensor setups (where information about the flow is collected) are trained with high-fidelity simulation data for a Reynolds number equal to approximately $300$ for 64 objects randomly generated using Bezier curves. The performance of the models and sensor setups are then assessed for the flow around 16 unseen objects. It is shown that our mapping approach improves percentage errors by up to 15\% in SMGFR when compared to a more conventional approach where the models are trained on a Cartesian grid. Finally, the SMGFR task is extended to predictions of fluid flow snapshots in the future, introducing the Spatio-temporal MGFR (STMGFR) task. For this spatio-temporal reconstruction task, a novel approach is developed involving splitting DNNs into a spatial and a temporal component. Our results demonstrate that this approach is able to reproduce, in time and in space, the main features of a fluid flow around arbitrary objects.

Poisson CNN: Convolutional Neural Networks for the Solution of the Poisson Equation with Varying Meshes and Dirichlet Boundary Conditions

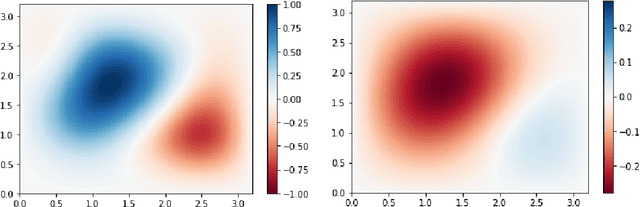
The Poisson equation is commonly encountered in engineering, including in computational fluid dynamics where it is needed to compute corrections to the pressure field. We propose a novel fully convolutional neural network (CNN) architecture to infer the solution of the Poisson equation on a 2D Cartesian grid of varying size and spacing given the right hand side term, arbitrary Dirichlet boundary conditions and grid parameters which provides unprecendented versatility in this application. The boundary conditions are handled using a novel approach by decomposing the original Poisson problem into a homogeneous Poisson problem plus four inhomogeneous Laplace sub-problems. The model is trained using a novel loss function approximating the continuous $L^p$ norm between the prediction and the target. Analytical test cases indicate that our CNN architecture is capable of predicting the correct solution of a Poisson problem with mean percentage errors of 15% and promises improvements in wall-clock runtimes for large problems. Furthermore, even when predicting on meshes denser than previously encountered, our model demonstrates encouraging capacity to reproduce the correct solution profile.