Emulating the Human Mind: A Neural-symbolic Link Prediction Model with Fast and Slow Reasoning and Filtered Rules

Link prediction is an important task in addressing the incompleteness problem of knowledge graphs (KG). Previous link prediction models suffer from issues related to either performance or explanatory capability. Furthermore, models that are capable of generating explanations, often struggle with erroneous paths or reasoning leading to the correct answer. To address these challenges, we introduce a novel Neural-Symbolic model named FaSt-FLiP (stands for Fast and Slow Thinking with Filtered rules for Link Prediction task), inspired by two distinct aspects of human cognition: "commonsense reasoning" and "thinking, fast and slow." Our objective is to combine a logical and neural model for enhanced link prediction. To tackle the challenge of dealing with incorrect paths or rules generated by the logical model, we propose a semi-supervised method to convert rules into sentences. These sentences are then subjected to assessment and removal of incorrect rules using an NLI (Natural Language Inference) model. Our approach to combining logical and neural models involves first obtaining answers from both the logical and neural models. These answers are subsequently unified using an Inference Engine module, which has been realized through both algorithmic implementation and a novel neural model architecture. To validate the efficacy of our model, we conducted a series of experiments. The results demonstrate the superior performance of our model in both link prediction metrics and the generation of more reliable explanations.

New Algebraic Normative Theories for Ethical and Legal Reasoning in the LogiKEy Framework

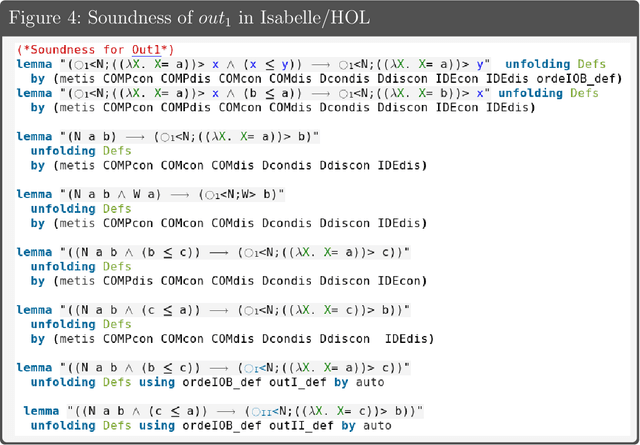
To design and engineer ethical and legal reasoners and responsible systems, Benzm\"{u}ller, Parent and van der Torre introduce LogiKEy methodology based on the semantical embedding of deontic logics into classic higher-order logic. In this paper, we considerably extend the LogiKEy deontic logics and dataset using an algebraic approach. We develop theory of input/output operations for normative reasoning on top of Boolean algebras.

Faithful Semantical Embedding of a Dyadic Deontic Logic in HOL

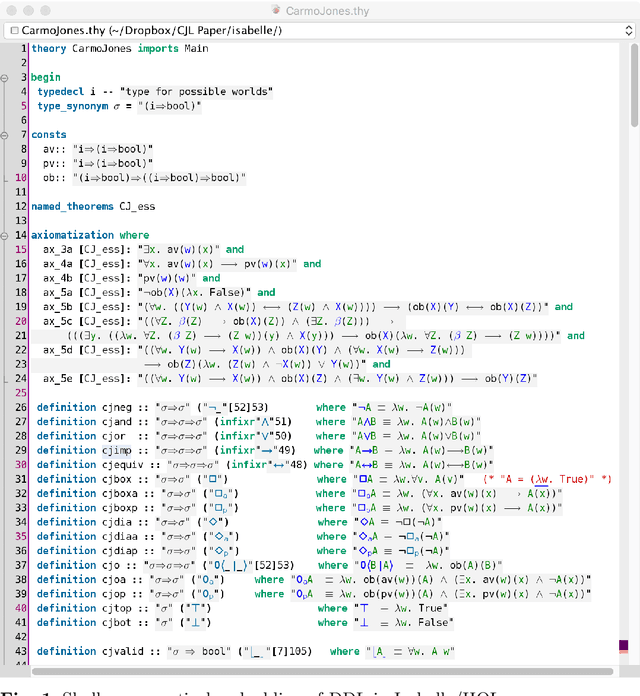
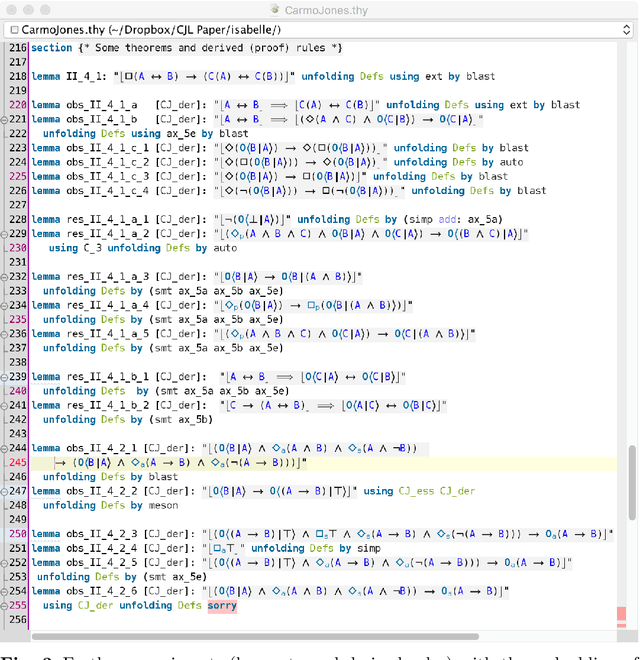
A shallow semantical embedding of a dyadic deontic logic by Carmo and Jones in classical higher-order logic is presented. This embedding is proven sound and complete, that is, faithful. The work presented here provides the theoretical foundation for the implementation and automation of dyadic deontic logic within off-the-shelf higher-order theorem provers and proof assistants.