Provable Reduction in Communication Rounds for Non-Smooth Convex Federated Learning

Multiple local steps are key to communication-efficient federated learning. However, theoretical guarantees for such algorithms, without data heterogeneity-bounding assumptions, have been lacking in general non-smooth convex problems. Leveraging projection-efficient optimization methods, we propose FedMLS, a federated learning algorithm with provable improvements from multiple local steps. FedMLS attains an $\epsilon$-suboptimal solution in $\mathcal{O}(1/\epsilon)$ communication rounds, requiring a total of $\mathcal{O}(1/\epsilon^2)$ stochastic subgradient oracle calls.

Federated Frank-Wolfe Algorithm

Federated learning (FL) has gained a lot of attention in recent years for building privacy-preserving collaborative learning systems. However, FL algorithms for constrained machine learning problems are still limited, particularly when the projection step is costly. To this end, we propose a Federated Frank-Wolfe Algorithm (FedFW). FedFW features data privacy, low per-iteration cost, and communication of sparse signals. In the deterministic setting, FedFW achieves an $\varepsilon$-suboptimal solution within $O(\varepsilon^{-2})$ iterations for smooth and convex objectives, and $O(\varepsilon^{-3})$ iterations for smooth but non-convex objectives. Furthermore, we present a stochastic variant of FedFW and show that it finds a solution within $O(\varepsilon^{-3})$ iterations in the convex setting. We demonstrate the empirical performance of FedFW on several machine learning tasks.

Personalized Multi-tier Federated Learning

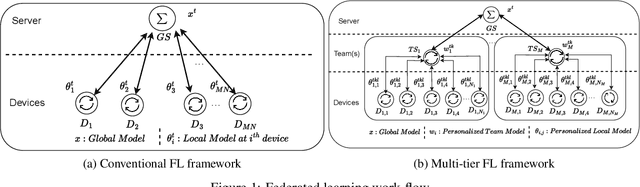
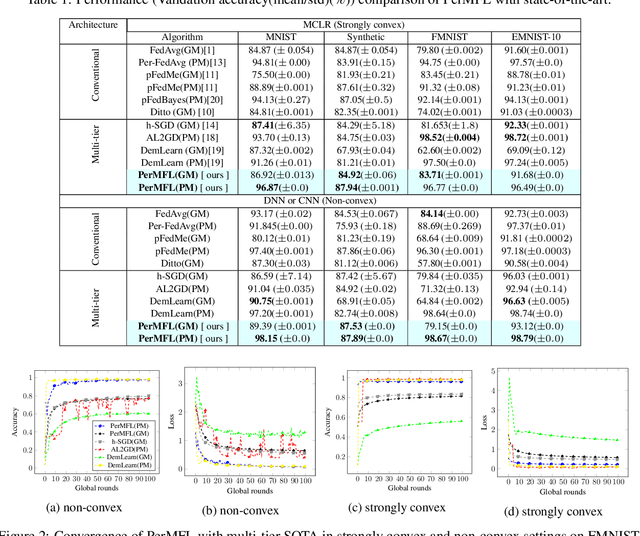
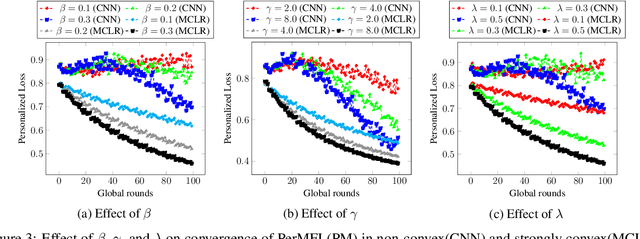
The key challenge of personalized federated learning (PerFL) is to capture the statistical heterogeneity properties of data with inexpensive communications and gain customized performance for participating devices. To address these, we introduced personalized federated learning in multi-tier architecture (PerMFL) to obtain optimized and personalized local models when there are known team structures across devices. We provide theoretical guarantees of PerMFL, which offers linear convergence rates for smooth strongly convex problems and sub-linear convergence rates for smooth non-convex problems. We conduct numerical experiments demonstrating the robust empirical performance of PerMFL, outperforming the state-of-the-art in multiple personalized federated learning tasks.

A Ridgelet Approach to Poisson Denoising

This paper introduces a novel ridgelet transform-based method for Poisson image denoising. Our work focuses on harnessing the Poisson noise's unique non-additive and signal-dependent properties, distinguishing it from Gaussian noise. The core of our approach is a new thresholding scheme informed by theoretical insights into the ridgelet coefficients of Poisson-distributed images and adaptive thresholding guided by Stein's method. We verify our theoretical model through numerical experiments and demonstrate the potential of ridgelet thresholding across assorted scenarios. Our findings represent a significant step in enhancing the understanding of Poisson noise and offer an effective denoising method for images corrupted with it.