Sensitivities: An Alternative to Conditional Probabilities for Bayesian Belief Networks

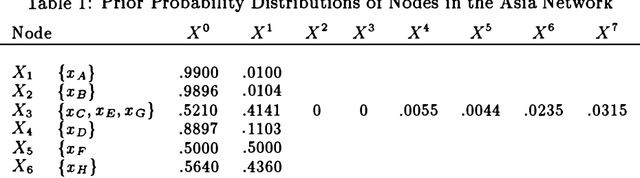
We show an alternative way of representing a Bayesian belief network by sensitivities and probability distributions. This representation is equivalent to the traditional representation by conditional probabilities, but makes dependencies between nodes apparent and intuitively easy to understand. We also propose a QR matrix representation for the sensitivities and/or conditional probabilities which is more efficient, in both memory requirements and computational speed, than the traditional representation for computer-based implementations of probabilistic inference. We use sensitivities to show that for a certain class of binary networks, the computation time for approximate probabilistic inference with any positive upper bound on the error of the result is independent of the size of the network. Finally, as an alternative to traditional algorithms that use conditional probabilities, we describe an exact algorithm for probabilistic inference that uses the QR-representation for sensitivities and updates probability distributions of nodes in a network according to messages from the neighbors.

Computational Complexity Reduction for BN2O Networks Using Similarity of States

Although probabilistic inference in a general Bayesian belief network is an NP-hard problem, computation time for inference can be reduced in most practical cases by exploiting domain knowledge and by making approximations in the knowledge representation. In this paper we introduce the property of similarity of states and a new method for approximate knowledge representation and inference which is based on this property. We define two or more states of a node to be similar when the ratio of their probabilities, the likelihood ratio, does not depend on the instantiations of the other nodes in the network. We show that the similarity of states exposes redundancies in the joint probability distribution which can be exploited to reduce the computation time of probabilistic inference in networks with multiple similar states, and that the computational complexity in the networks with exponentially many similar states might be polynomial. We demonstrate our ideas on the example of a BN2O network -- a two layer network often used in diagnostic problems -- by reducing it to a very close network with multiple similar states. We show that the answers to practical queries converge very fast to the answers obtained with the original network. The maximum error is as low as 5% for models that require only 10% of the computation time needed by the original BN2O model.

Nonuniform Dynamic Discretization in Hybrid Networks

We consider probabilistic inference in general hybrid networks, which include continuous and discrete variables in an arbitrary topology. We reexamine the question of variable discretization in a hybrid network aiming at minimizing the information loss induced by the discretization. We show that a nonuniform partition across all variables as opposed to uniform partition of each variable separately reduces the size of the data structures needed to represent a continuous function. We also provide a simple but efficient procedure for nonuniform partition. To represent a nonuniform discretization in the computer memory, we introduce a new data structure, which we call a Binary Split Partition (BSP) tree. We show that BSP trees can be an exponential factor smaller than the data structures in the standard uniform discretization in multiple dimensions and show how the BSP trees can be used in the standard join tree algorithm. We show that the accuracy of the inference process can be significantly improved by adjusting discretization with evidence. We construct an iterative anytime algorithm that gradually improves the quality of the discretization and the accuracy of the answer on a query. We provide empirical evidence that the algorithm converges.