Sensitivities: An Alternative to Conditional Probabilities for Bayesian Belief Networks
Paper and Code
Feb 20, 2013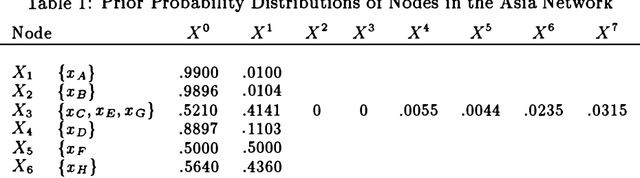

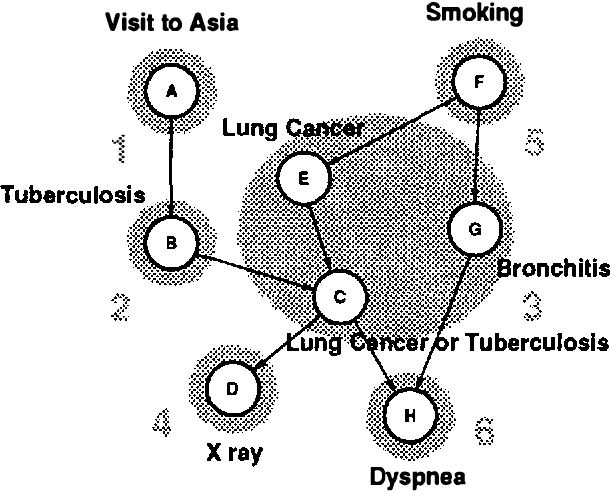
We show an alternative way of representing a Bayesian belief network by sensitivities and probability distributions. This representation is equivalent to the traditional representation by conditional probabilities, but makes dependencies between nodes apparent and intuitively easy to understand. We also propose a QR matrix representation for the sensitivities and/or conditional probabilities which is more efficient, in both memory requirements and computational speed, than the traditional representation for computer-based implementations of probabilistic inference. We use sensitivities to show that for a certain class of binary networks, the computation time for approximate probabilistic inference with any positive upper bound on the error of the result is independent of the size of the network. Finally, as an alternative to traditional algorithms that use conditional probabilities, we describe an exact algorithm for probabilistic inference that uses the QR-representation for sensitivities and updates probability distributions of nodes in a network according to messages from the neighbors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge