Bayesian inference of composition-dependent phase diagrams

Phase diagrams serve as a highly informative tool for materials design, encapsulating information about the phases that a material can manifest under specific conditions. In this work, we develop a method in which Bayesian inference is employed to combine thermodynamic data from molecular dynamics (MD), melting point simulations, and phonon calculations, process these data, and yield a temperature-concentration phase diagram. The employed Bayesian framework yields us not only the free energies of different phases as functions of temperature and concentration but also the uncertainties of these free energies originating from statistical errors inherent to finite-length MD trajectories. Furthermore, it extrapolates the results of the finite-atom calculations to the infinite-atom limit and facilitates the choice of temperature, chemical potentials, and the number of atoms conducting the next simulation with which will be the most efficient in reducing the uncertainty of the phase diagram. The developed algorithm was successfully tested on two binary systems, Ge-Si and K-Na, in the full range of concentrations and temperatures.

A physics-informed AI method for calculating melting points with uncertainty control and optimal sampling

We present an artificial intelligence (AI) method for automatically computing the melting point based on coexistence simulations in the NPT ensemble. Given the interatomic interaction model, the method makes decisions regarding the number of atoms and temperature at which to conduct simulations, and based on the collected data predicts the melting point along with the uncertainty, which can be systematically improved with more data. We demonstrate how incorporating physical models of the solid-liquid coexistence evolution enhances the AI method's accuracy and enables optimal decision-making to effectively reduce predictive uncertainty. To validate our approach, we compare our results with approximately 20 melting point calculations from the literature. Remarkably, we observe significant deviations in about one-third of the cases, underscoring the need for accurate and reliable AI-based algorithms for materials property calculations.

Deeper Connections between Neural Networks and Gaussian Processes Speed-up Active Learning

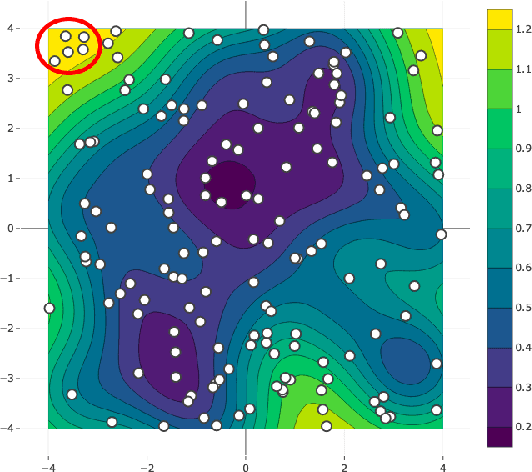
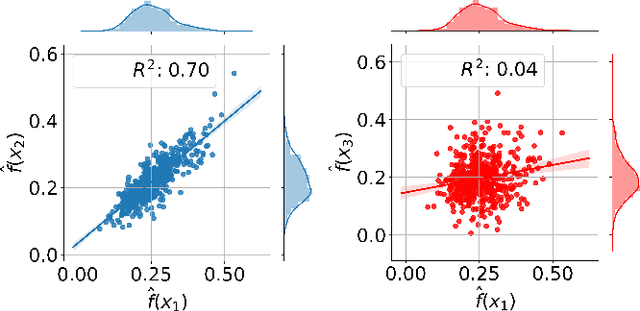
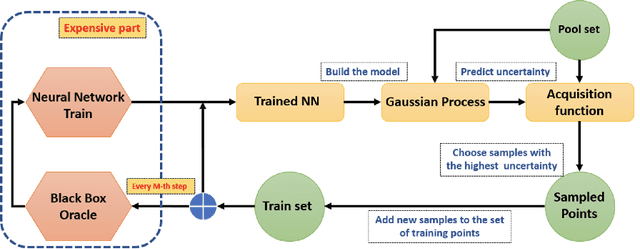
Active learning methods for neural networks are usually based on greedy criteria which ultimately give a single new design point for the evaluation. Such an approach requires either some heuristics to sample a batch of design points at one active learning iteration, or retraining the neural network after adding each data point, which is computationally inefficient. Moreover, uncertainty estimates for neural networks sometimes are overconfident for the points lying far from the training sample. In this work we propose to approximate Bayesian neural networks (BNN) by Gaussian processes, which allows us to update the uncertainty estimates of predictions efficiently without retraining the neural network, while avoiding overconfident uncertainty prediction for out-of-sample points. In a series of experiments on real-world data including large-scale problems of chemical and physical modeling, we show superiority of the proposed approach over the state-of-the-art methods.

Dropout-based Active Learning for Regression

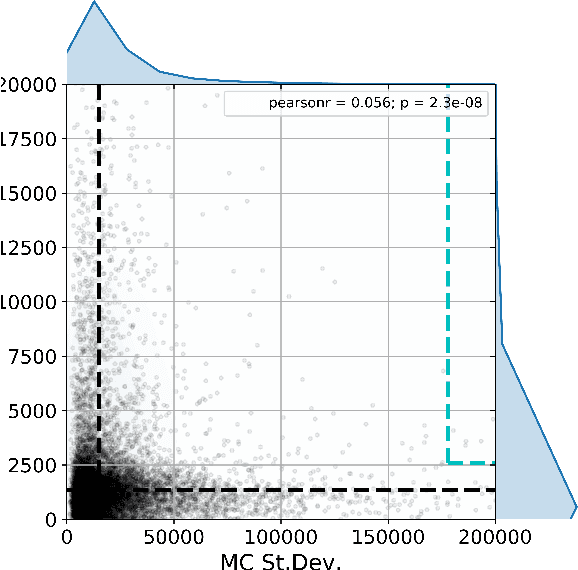
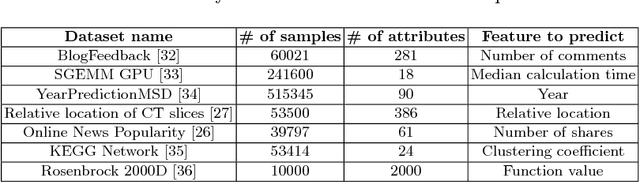
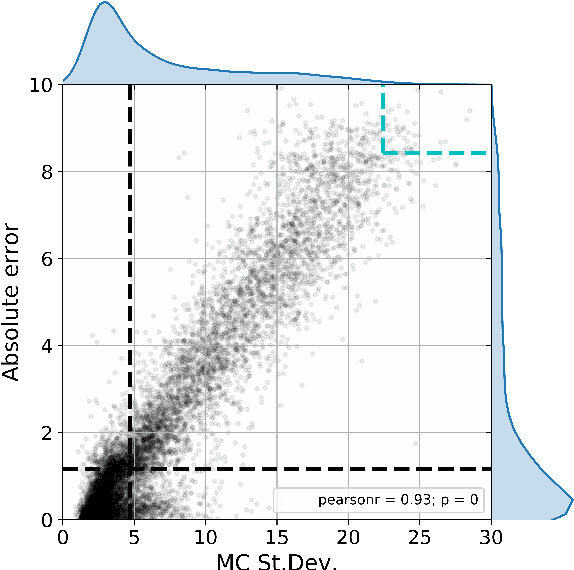
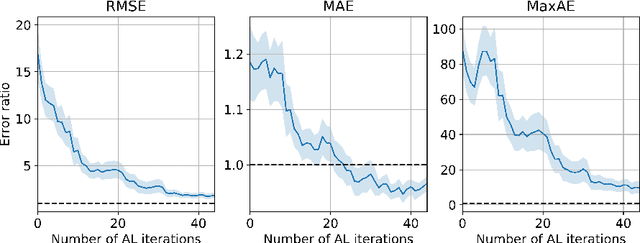
Active learning is relevant and challenging for high-dimensional regression models when the annotation of the samples is expensive. Yet most of the existing sampling methods cannot be applied to large-scale problems, consuming too much time for data processing. In this paper, we propose a fast active learning algorithm for regression, tailored for neural network models. It is based on uncertainty estimation from stochastic dropout output of the network. Experiments on both synthetic and real-world datasets show comparable or better performance (depending on the accuracy metric) as compared to the baselines. This approach can be generalized to other deep learning architectures. It can be used to systematically improve a machine-learning model as it offers a computationally efficient way of sampling additional data.