On the practical applicability of modern DFT functionals for chemical computations. Case study of DM21 applicability for geometry optimization

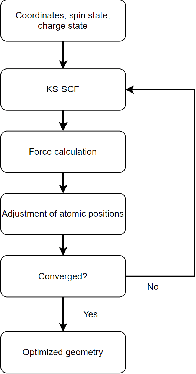
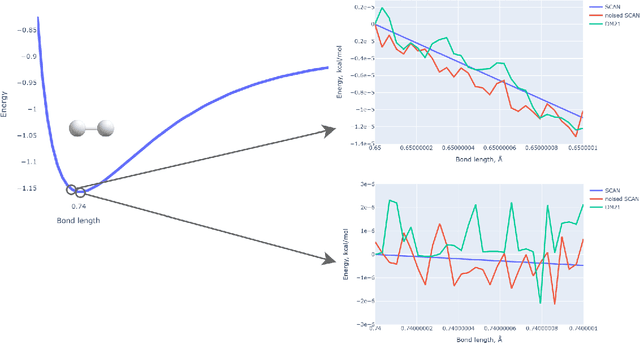
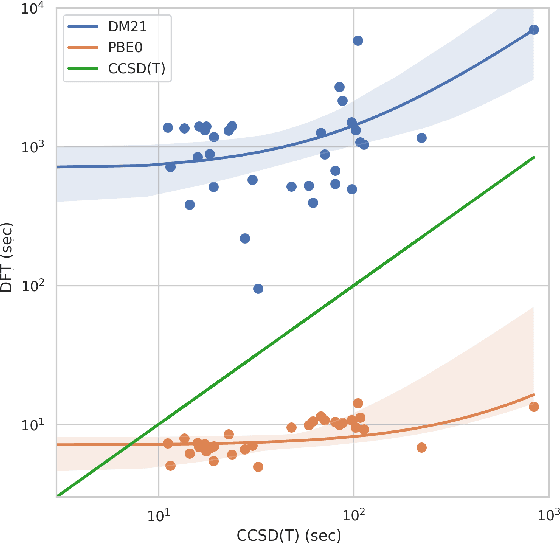
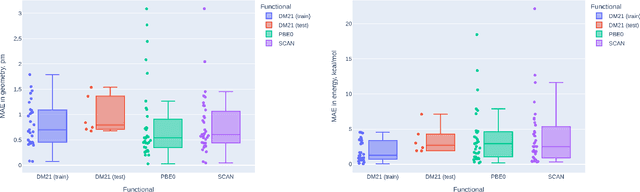
Density functional theory (DFT) is probably the most promising approach for quantum chemistry calculations considering its good balance between calculations precision and speed. In recent years, several neural network-based functionals have been developed for exchange-correlation energy approximation in DFT, DM21 developed by Google Deepmind being the most notable between them. This study focuses on evaluating the efficiency of DM21 functional in predicting molecular geometries, with a focus on the influence of oscillatory behavior in neural network exchange-correlation functionals. We implemented geometry optimization in PySCF for the DM21 functional in geometry optimization problem, compared its performance with traditional functionals, and tested it on various benchmarks. Our findings reveal both the potential and the current challenges of using neural network functionals for geometry optimization in DFT. We propose a solution extending the practical applicability of such functionals and allowing to model new substances with their help.

A Method for Auto-Differentiation of the Voronoi Tessellation

Voronoi tessellation, also known as Voronoi diagram, is an important computational geometry technique that has applications in various scientific disciplines. It involves dividing a given space into regions based on the proximity to a set of points. Autodifferentiation is a powerful tool for solving optimization tasks. Autodifferentiation assumes constructing a computational graph that allows to compute gradients using backpropagation algorithm. However, often the Voronoi tessellation remains the only non-differentiable part of a pipeline, prohibiting end-to-end differentiation. We present the method for autodifferentiation of the 2D Voronoi tessellation. The method allows one to construct the Voronoi tessellation and pass gradients, making the construction end-to-end differentiable. We provide the implementation details and present several important applications. To the best of our knowledge this is the first autodifferentiable realization of the Voronoi tessellation providing full set of Voronoi geometrical parameters in a differentiable way.