Redundancy Parameterization of the ABB YuMi Robot Arm

The ABB YuMi is a 7-DOF collaborative robot arm with a complex, redundant kinematic structure. Path planning for the YuMi is challenging, especially with joint limits considered. The redundant degree of freedom is parameterized by the Shoulder-Elbow-Wrist (SEW) angle, called the arm angle by ABB, but the exact definition must be known for path planning outside the RobotStudio simulator. We provide the first complete and validated definition of the SEW angle used for the YuMi. It follows the conventional SEW angle formulation with the shoulder-elbow direction chosen to be the direction of the fourth joint axis. Our definition also specifies the shoulder location, making it compatible with any choice of reference vector. A previous attempt to define the SEW angle exists in the literature, but it is incomplete and deviates from the behavior observed in RobotStudio. Because our formulation fits within the general SEW angle framework, we also obtain the expression for the SEW angle Jacobian and complete numerical conditions for all algorithmic singularities. Finally, we demonstrate using IK-Geo, our inverse kinematics (IK) solver based on subproblem decomposition, to find all IK solutions using 2D search. Code examples are available in a publicly accessible repository.

Path Planning and Optimization for Cuspidal 6R Manipulators

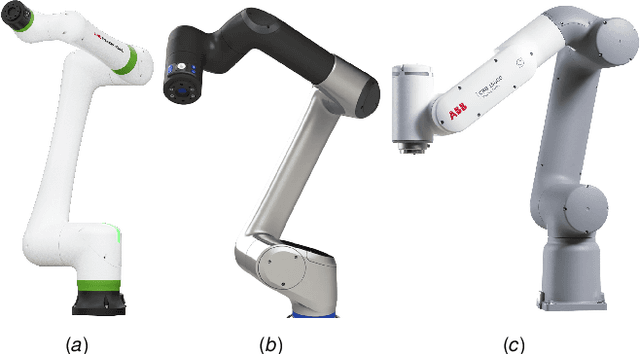
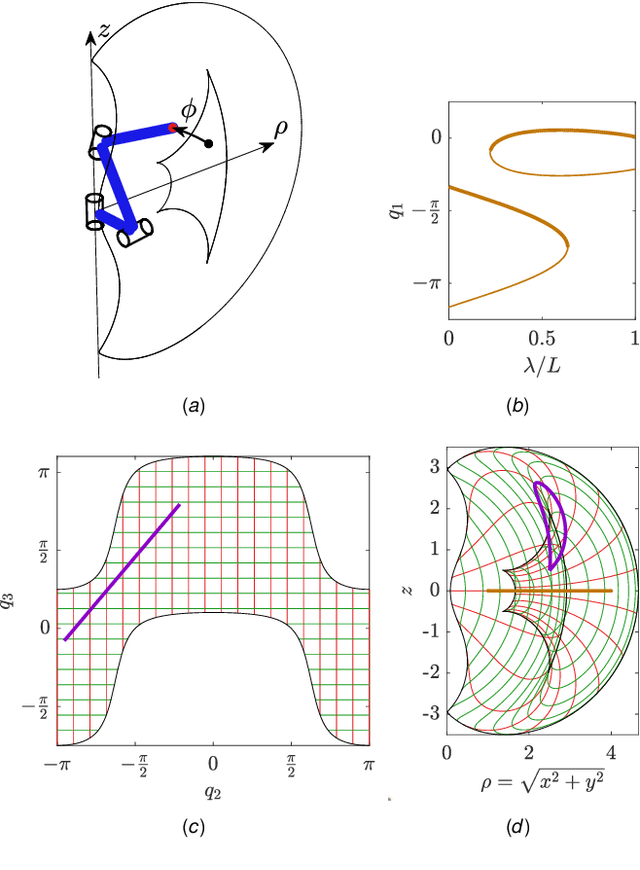
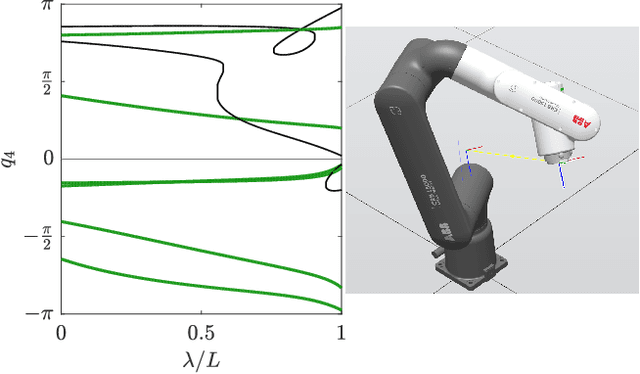
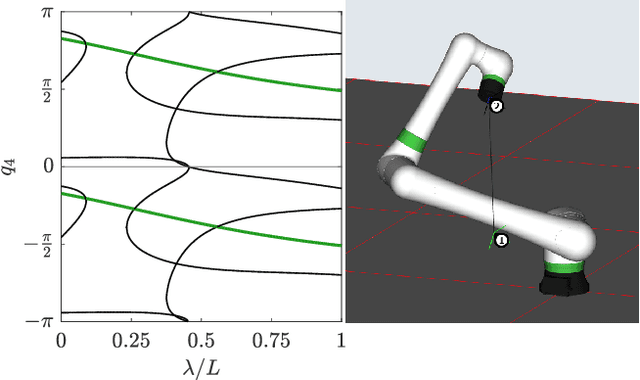
A cuspidal robot can move from one inverse kinematics (IK) solution to another without crossing a singularity. Multiple industrial robots are cuspidal. They tend to have a beautiful mechanical design, but they pose path planning challenges. A task-space path may have a valid IK solution for each point along the path, but a continuous joint-space path may depend on the choice of the IK solution or even be infeasible. This paper presents new analysis, path planning, and optimization methods to enhance the utility of cuspidal robots. We first demonstrate an efficient method to identify cuspidal robots and show, for the first time, that the ABB GoFa and certain robots with three parallel joint axes are cuspidal. We then propose a new path planning method for cuspidal robots by finding all IK solutions for each point along a task-space path and constructing a graph to connect each vertex corresponding to an IK solution. Graph edges are weighted based on the optimization metric, such as minimizing joint velocity. The optimal feasible path is the shortest path in the graph. This method can find non-singular paths as well as smooth paths which pass through singularities. Finally, this path planning method is incorporated into a path optimization algorithm. Given a fixed workspace toolpath, we optimize the offset of the toolpath in the robot base frame while ensuring continuous joint motion. Code examples are available in a publicly accessible repository.

Redundancy parameterization and inverse kinematics of 7-DOF revolute manipulators

Seven degree-of-freedom (DOF) robot arms have one redundant DOF which does not change the translational or rotational motion of the end effector. The redundant DOF offers greater manipulability of the arm configuration to avoid obstacles and steer away from singularities, but it must be parameterized to fully specify the joint angles for a given end effector pose. For 7-DOF revolute (7R) manipulators, we introduce a new concept of generalized shoulder-elbow-wrist (SEW) angle, a generalization of the conventional SEW angle but with an arbitrary choice of the reference direction function. The SEW angle is easy for human operators to visualize as a rotation of the elbow about the line from the shoulder to the wrist and has been used in the teleoperation of space robot arms. Since the conventional SEW angle formulation is prone to singularities, we introduce a special choice of the reference direction function called the stereographic SEW angle which has a singularity in only one direction in the workspace. We prove that such a singularity is unavoidable for any parameterization. We also include expressions for the SEW angle Jacobian along with singularity analysis. Finally, we provide inverse kinematics solutions for most known 7R manipulators using the general SEW angle and the subproblem decomposition method. These solutions are often closed-form but may sometimes involve a 1D or 2D search. Inverse kinematics solutions, examples, and evaluations are available in a publicly accessible repository.

Canonical Subproblems for Robot Inverse Kinematics

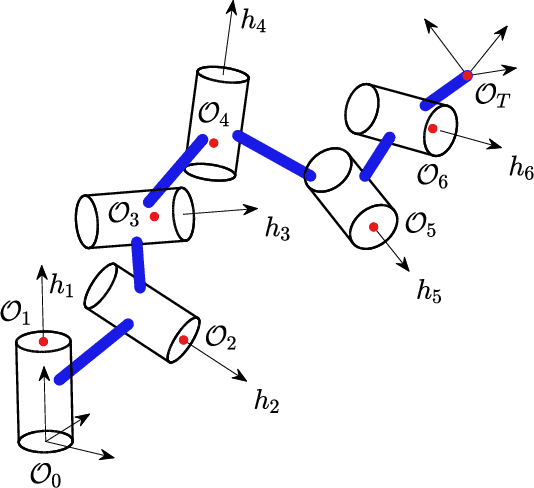
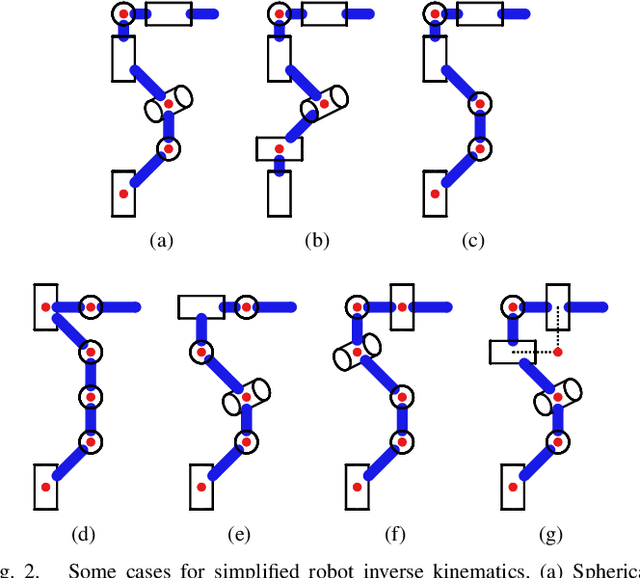
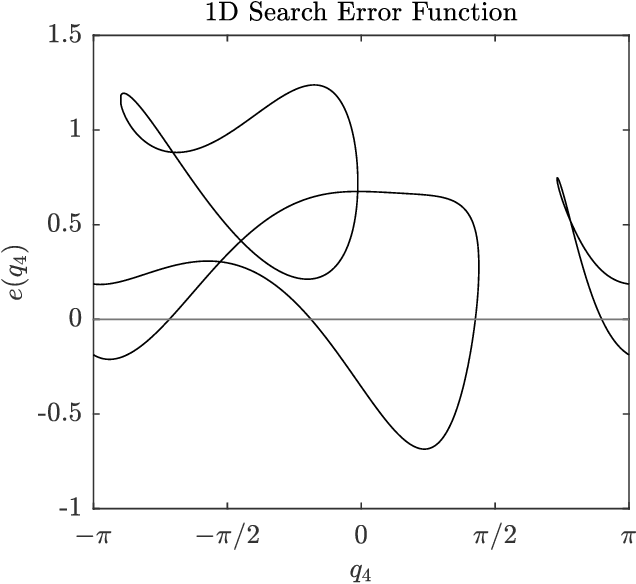
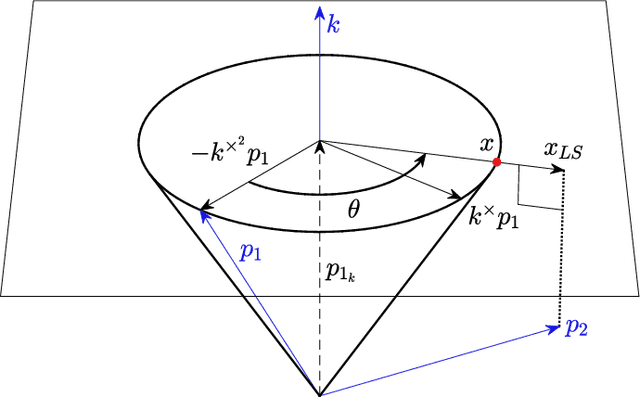
Inverse kinematics of many common types of robot manipulators may be decomposed into canonical subproblems. This paper presents new solution methods to six subproblems using a linear algebra approach. The first three subproblems, called the Paden-Kahan subproblems, are Subproblem 1: angle between a vector on the edge of a cone and a point, Subproblem 2: intersections between two cones, and Subproblem 3: intersections between a cone and a sphere. The other three subproblems, which have not been extensively covered in the literature, are Subproblem 4: intersections between a cone and a plane, Subproblem 5: intersections among three cones, and Subproblem 6: intersections in a system of four cones. We present algebraic solutions and geometric interpretations for each subproblem and provide computational performance comparisons. Our approach also finds the least-squares solutions for Subproblems 1-4 when the exact solution does not exist. We show that almost all 6-dof all revolute (6R) robots with known closed-form solutions may be solved using the subproblem decomposition method. For a general 6R robot, subproblem decomposition reduces finding all solutions to a search on a circle or a 2D torus. The software code is available on a publicly accessible repository.