Fighting Quantization Bias With Bias

Low-precision representation of deep neural networks (DNNs) is critical for efficient deployment of deep learning application on embedded platforms, however, converting the network to low precision degrades its performance. Crucially, networks that are designed for embedded applications usually suffer from increased degradation since they have less redundancy. This is most evident for the ubiquitous MobileNet architecture which requires a costly quantization-aware training cycle to achieve acceptable performance when quantized to 8-bits. In this paper, we trace the source of the degradation in MobileNets to a shift in the mean activation value. This shift is caused by an inherent bias in the quantization process which builds up across layers, shifting all network statistics away from the learned distribution. We show that this phenomenon happens in other architectures as well. We propose a simple remedy - compensating for the quantization induced shift by adding a constant to the additive bias term of each channel. We develop two simple methods for estimating the correction constants - one using iterative evaluation of the quantized network and one where the constants are set using a short training phase. Both methods are fast and require only a small amount of unlabeled data, making them appealing for rapid deployment of neural networks. Using the above methods we are able to match the performance of training-based quantization of MobileNets at a fraction of the cost.

Same, Same But Different - Recovering Neural Network Quantization Error Through Weight Factorization

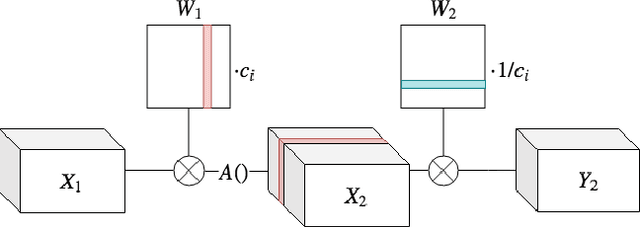
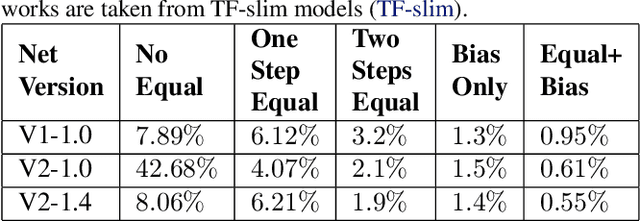
Quantization of neural networks has become common practice, driven by the need for efficient implementations of deep neural networks on embedded devices. In this paper, we exploit an oft-overlooked degree of freedom in most networks - for a given layer, individual output channels can be scaled by any factor provided that the corresponding weights of the next layer are inversely scaled. Therefore, a given network has many factorizations which change the weights of the network without changing its function. We present a conceptually simple and easy to implement method that uses this property and show that proper factorizations significantly decrease the degradation caused by quantization. We show improvement on a wide variety of networks and achieve state-of-the-art degradation results for MobileNets. While our focus is on quantization, this type of factorization is applicable to other domains such as network-pruning, neural nets regularization and network interpretability.