Alex Cuozzo
Sequential change-point detection for mutually exciting point processes over networks
Feb 10, 2021
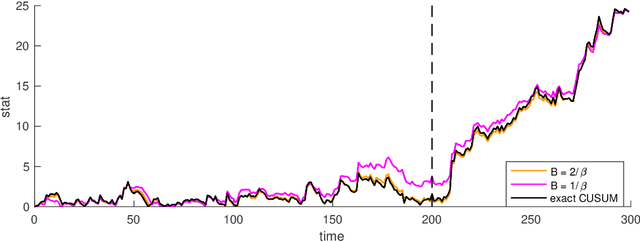
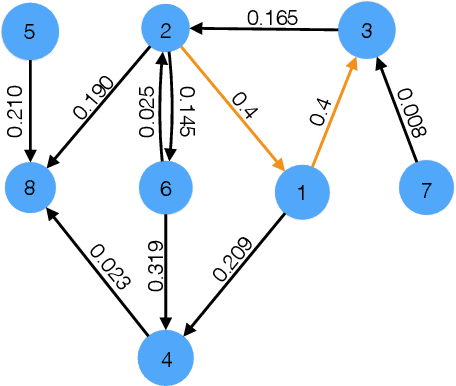
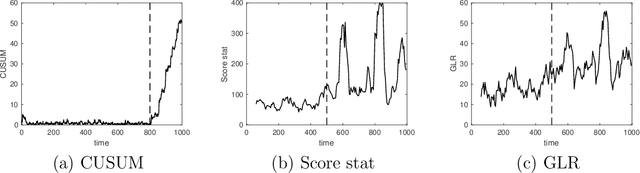
Abstract:We present a new CUSUM procedure for sequentially detecting change-point in the self and mutual exciting processes, a.k.a. Hawkes networks using discrete events data. Hawkes networks have become a popular model for statistics and machine learning due to their capability in modeling irregularly observed data where the timing between events carries a lot of information. The problem of detecting abrupt changes in Hawkes networks arises from various applications, including neuronal imaging, sensor network, and social network monitoring. Despite this, there has not been a computationally and memory-efficient online algorithm for detecting such changes from sequential data. We present an efficient online recursive implementation of the CUSUM statistic for Hawkes processes, both decentralized and memory-efficient, and establish the theoretical properties of this new CUSUM procedure. We then show that the proposed CUSUM method achieves better performance than existing methods, including the Shewhart procedure based on count data, the generalized likelihood ratio (GLR) in the existing literature, and the standard score statistic. We demonstrate this via a simulated example and an application to population code change-detection in neuronal networks.
Uncertainty Quantification for Inferring Hawkes Networks
Jun 12, 2020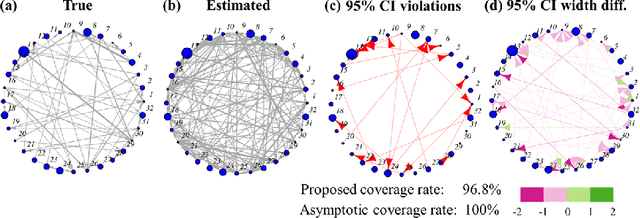
Abstract:Multivariate Hawkes processes are commonly used to model streaming networked event data in a wide variety of applications. However, it remains a challenge to extract reliable inference from complex datasets with uncertainty quantification. Aiming towards this, we develop a statistical inference framework to learn causal relationships between nodes from networked data, where the underlying directed graph implies Granger causality. We provide uncertainty quantification for the maximum likelihood estimate of the network multivariate Hawkes process by providing a non-asymptotic confidence set. The main technique is based on the concentration inequalities of continuous-time martingales. We compare our method to the previously-derived asymptotic Hawkes process confidence interval, and demonstrate the strengths of our method in an application to neuronal connectivity reconstruction.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge