Kernel learning approaches for summarising and combining posterior similarity matrices

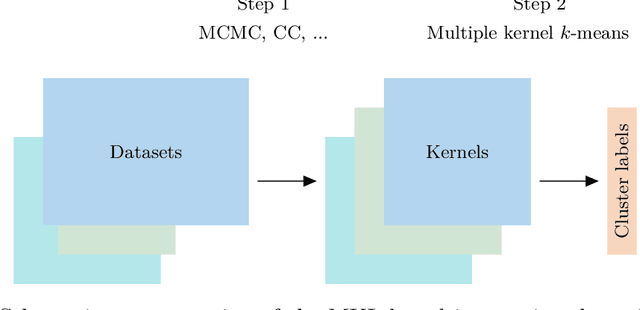
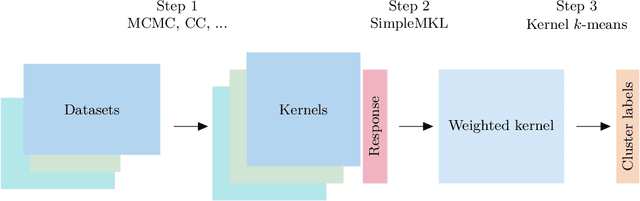
When using Markov chain Monte Carlo (MCMC) algorithms to perform inference for Bayesian clustering models, such as mixture models, the output is typically a sample of clusterings (partitions) drawn from the posterior distribution. In practice, a key challenge is how to summarise this output. Here we build upon the notion of the posterior similarity matrix (PSM) in order to suggest new approaches for summarising the output of MCMC algorithms for Bayesian clustering models. A key contribution of our work is the observation that PSMs are positive semi-definite, and hence can be used to define probabilistically-motivated kernel matrices that capture the clustering structure present in the data. This observation enables us to employ a range of kernel methods to obtain summary clusterings, and otherwise exploit the information summarised by PSMs. For example, if we have multiple PSMs, each corresponding to a different dataset on a common set of statistical units, we may use standard methods for combining kernels in order to perform integrative clustering. We may moreover embed PSMs within predictive kernel models in order to perform outcome-guided data integration. We demonstrate the performances of the proposed methods through a range of simulation studies as well as two real data applications. R code is available at https://github.com/acabassi/combine-psms.

Two-step penalised logistic regression for multi-omic data with an application to cardiometabolic syndrome

Building classification models that predict a binary class label on the basis of high dimensional multi-omics datasets poses several challenges, due to the typically widely differing characteristics of the data layers in terms of number of predictors, type of data, and levels of noise. Previous research has shown that applying classical logistic regression with elastic-net penalty to these datasets can lead to poor results (Liu et al., 2018). We implement a two-step approach to multi-omic logistic regression in which variable selection is performed on each layer separately and a predictive model is then built using the variables selected in the first step. Here, our approach is compared to other methods that have been developed for the same purpose, and we adapt existing software for multi-omic linear regression (Zhao and Zucknick, 2020) to the logistic regression setting. Extensive simulation studies show that our approach should be preferred if the goal is to select as many relevant predictors as possible, as well as achieving prediction performances comparable to those of the best competitors. Our motivating example is a cardiometabolic syndrome dataset comprising eight 'omic data types for 2 extreme phenotype groups (10 obese and 10 lipodystrophy individuals) and 185 blood donors. Our proposed approach allows us to identify features that characterise cardiometabolic syndrome at the molecular level. R code is available at https://github.com/acabassi/logistic-regression-for-multi-omic-data.

Multiple kernel learning for integrative consensus clustering of genomic datasets

Diverse applications - particularly in tumour subtyping - have demonstrated the importance of integrative clustering as a means to combine information from multiple high-dimensional omics datasets. Cluster-Of-Clusters Analysis (COCA) is a popular integrative clustering method that has been widely applied in the context of tumour subtyping. However, the properties of COCA have never been systematically explored, and the robustness of this approach to the inclusion of noisy datasets, or datasets that define conflicting clustering structures, is unclear. We rigorously benchmark COCA, and present Kernel Learning Integrative Clustering (KLIC) as an alternative strategy. KLIC frames the challenge of combining clustering structures as a multiple kernel learning problem, in which different datasets each provide a weighted contribution to the final clustering. This allows the contribution of noisy datasets to be down-weighted relative to more informative datasets. We show through extensive simulation studies that KLIC is more robust than COCA in a variety of situations. R code to run KLIC and COCA can be found at https://github.com/acabassi/klic