Role of Spatial Coherence in Diffractive Optical Neural Networks

Diffractive optical neural networks (DONNs) have emerged as a promising optical hardware platform for ultra-fast and energy-efficient signal processing for machine learning tasks, particularly in computer vision. However, previous experimental demonstrations of DONNs have only been performed using coherent light, which is not present in the natural world. Here, we study the role of spatial optical coherence in DONN operation. We propose a numerical approach to efficiently simulate DONNs under input illumination with arbitrary spatial coherence and discuss the corresponding computational complexity using coherent, partially coherent, and incoherent light. We also investigate the expressive power of DONNs and examine how coherence affects their performance. In particular, we show that under fully incoherent illumination, the DONN performance cannot surpass that of a linear model. As a demonstration, we train and evaluate simulated DONNs on the MNIST dataset of handwritten digits using light with varying spatial coherence.

Autoregressive neural-network wavefunctions for ab initio quantum chemistry

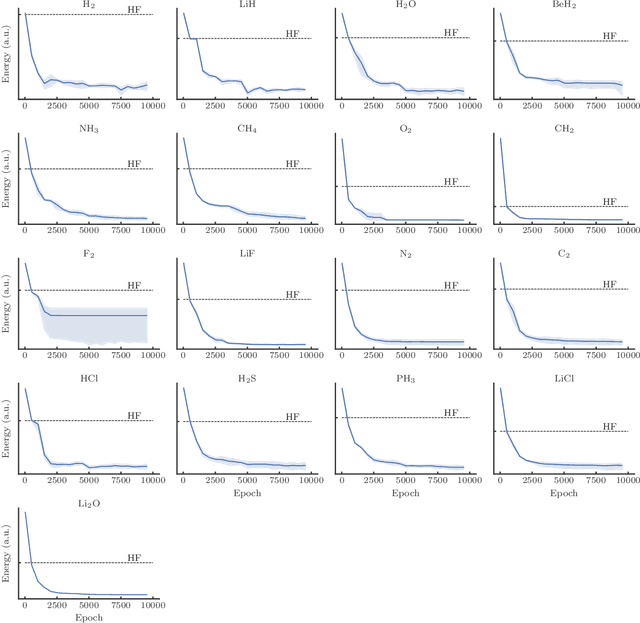
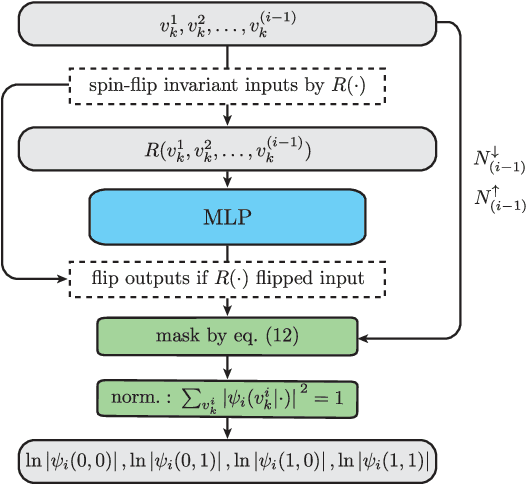
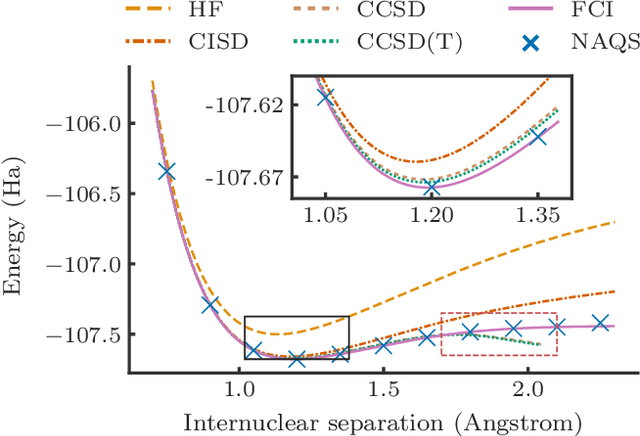
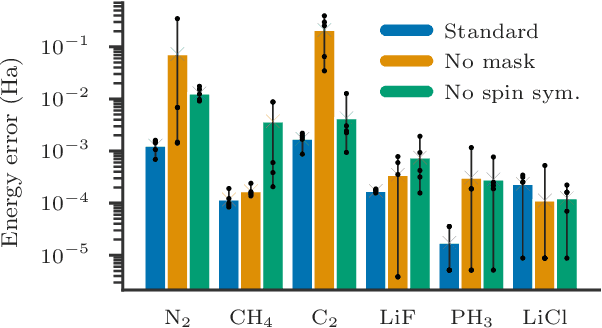
Performing electronic structure calculations is a canonical many-body problem that has recently emerged as a challenging new paradigm for neural network quantum states (NNQS). Here, we parameterise the electronic wavefunction with a novel autoregressive neural network (ARN) that permits highly efficient and scalable sampling, whilst also embedding physical priors that reflect the structure of molecular systems without sacrificing expressibility. This allows us to perform electronic structure calculations on molecules with up to 30 spin-orbitals - which consider multiple orders of magnitude more Slater determinants than previous applications of conventional NNQS - and we find that our ansatz can outperform the de-facto gold-standard coupled cluster methods even in the presence of strong quantum correlations. With a highly expressive neural network for which sampling is no longer a computational bottleneck, we conclude that the barriers to further scaling are not associated with the wavefunction ansatz itself, but rather are inherent to any variational Monte Carlo approach.