Data Fusion of Deep Learned Molecular Embeddings for Property Prediction

Data-driven approaches such as deep learning can result in predictive models for material properties with exceptional accuracy and efficiency. However, in many problems data is sparse, severely limiting their accuracy and applicability. To improve predictions, techniques such as transfer learning and multi-task learning have been used. The performance of multi-task learning models depends on the strength of the underlying correlations between tasks and the completeness of the dataset. We find that standard multi-task models tend to underperform when trained on sparse datasets with weakly correlated properties. To address this gap, we use data fusion techniques to combine the learned molecular embeddings of various single-task models and trained a multi-task model on this combined embedding. We apply this technique to a widely used benchmark dataset of quantum chemistry data for small molecules as well as a newly compiled sparse dataset of experimental data collected from literature and our own quantum chemistry and thermochemical calculations. The results show that the fused, multi-task models outperform standard multi-task models for sparse datasets and can provide enhanced prediction on data-limited properties compared to single-task models.

Multi-Task Multi-Fidelity Learning of Properties for Energetic Materials

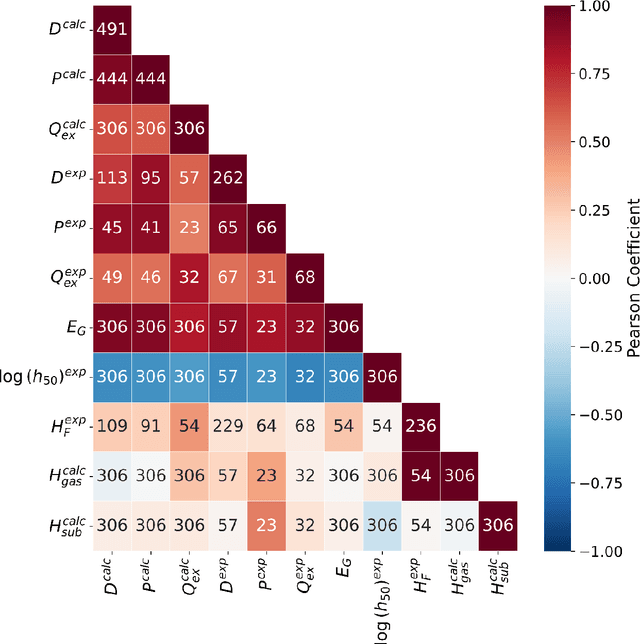
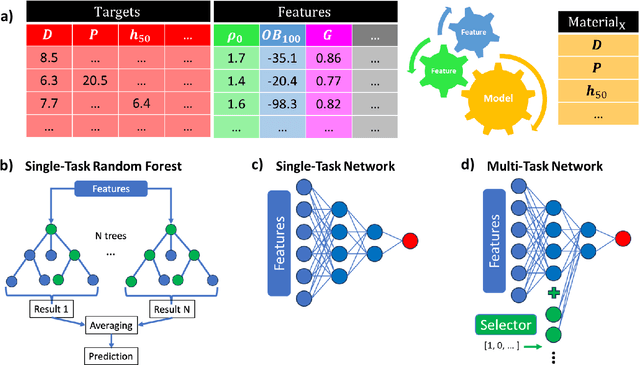
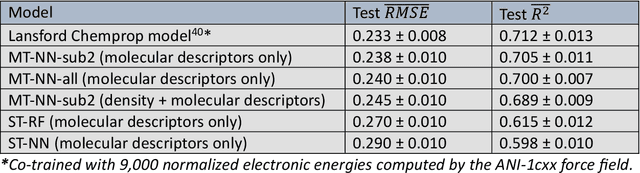
Data science and artificial intelligence are playing an increasingly important role in the physical sciences. Unfortunately, in the field of energetic materials data scarcity limits the accuracy and even applicability of ML tools. To address data limitations, we compiled multi-modal data: both experimental and computational results for several properties. We find that multi-task neural networks can learn from multi-modal data and outperform single-task models trained for specific properties. As expected, the improvement is more significant for data-scarce properties. These models are trained using descriptors built from simple molecular information and can be readily applied for large-scale materials screening to explore multiple properties simultaneously. This approach is widely applicable to fields outside energetic materials.

GPT-4 as an interface between researchers and computational software: improving usability and reproducibility

Large language models (LLMs) are playing an increasingly important role in science and engineering. For example, their ability to parse and understand human and computer languages makes them powerful interpreters and their use in applications like code generation are well-documented. We explore the ability of the GPT-4 LLM to ameliorate two major challenges in computational materials science: i) the high barriers for adoption of scientific software associated with the use of custom input languages, and ii) the poor reproducibility of published results due to insufficient details in the description of simulation methods. We focus on a widely used software for molecular dynamics simulations, the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS), and quantify the usefulness of input files generated by GPT-4 from task descriptions in English and its ability to generate detailed descriptions of computational tasks from input files. We find that GPT-4 can generate correct and ready-to-use input files for relatively simple tasks and useful starting points for more complex, multi-step simulations. In addition, GPT-4's description of computational tasks from input files can be tuned from a detailed set of step-by-step instructions to a summary description appropriate for publications. Our results show that GPT-4 can reduce the number of routine tasks performed by researchers, accelerate the training of new users, and enhance reproducibility.

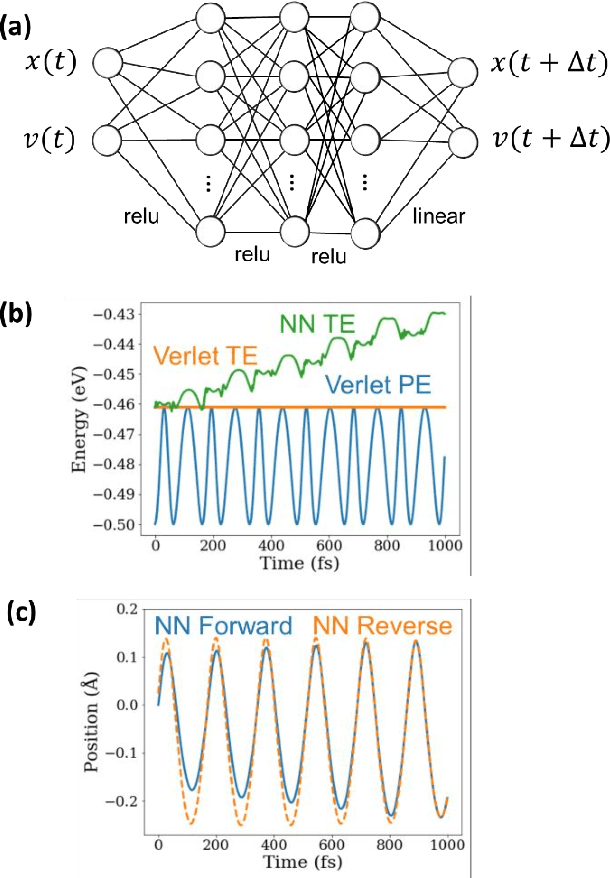
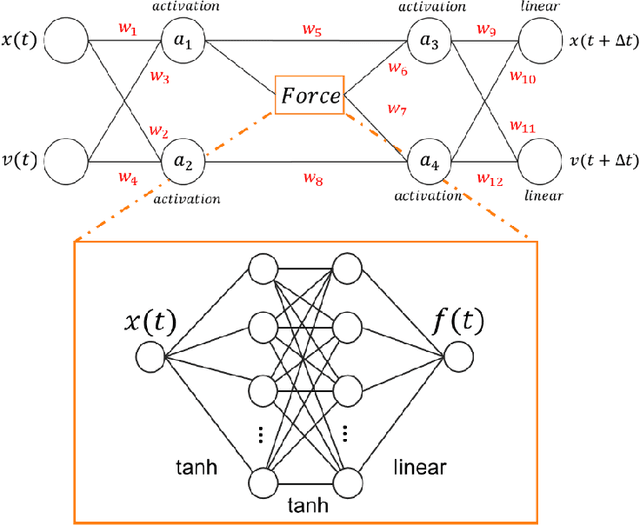
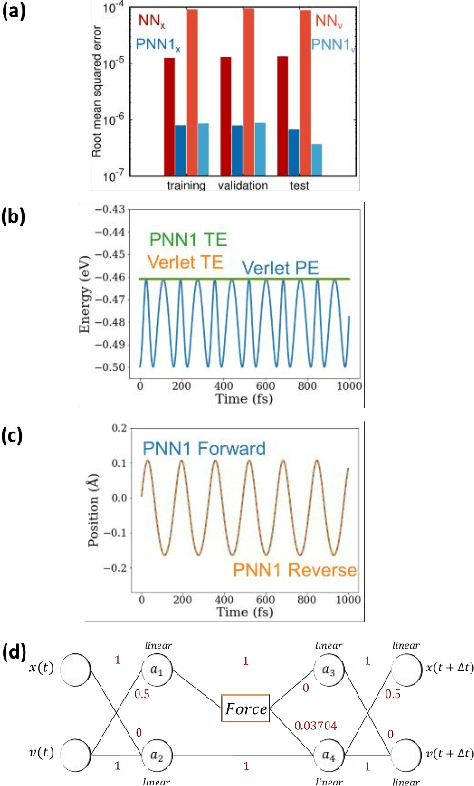
Parsimonious neural networks learn classical mechanics and can teach it

We combine neural networks with genetic algorithms to find parsimonious models that describe the time evolution of a point particle subjected to an external potential. The genetic algorithm is designed to find the simplest, most interpretable network compatible with the training data. The parsimonious neural network (PNN) can numerically integrate classical equations of motion with negligible energy drifts and good time reversibility, significantly outperforming a generic feed-forward neural network. Our PNN is immediately interpretable as the position Verlet algorithm, a non-trivial integrator whose justification originates from Trotter's theorem.