A Novel Comprehensive Multiport Network Model for Stacked Intelligent Metasurfaces (SIM) Characterization and OptimizationA

Reconfigurable Intelligent Surfaces (RIS) are transformative technologies for next-generation wireless communication, offering advanced control over electromagnetic wave propagation. While RIS have been extensively studied, Stacked Intelligent Metasurfaces (SIM), which extend the RIS concept to multi-layered systems, present significant modeling and optimization challenges. This work addresses these challenges by introducing a new optimization framework for heterogeneous SIM architectures that, compared to previous approaches, is based on a comprehensive model without relying on specific assumptions, allowing for a broader applicability of the results. To this end, we first present a model based on multi-port network theory for characterizing a general electromagnetic collaborative object (ECO) and derive a general framework for ECO optimization. We then introduce the SIM as an ECO with a specific architecture and provide insights into SIM optimization for various architectures, discussing the complexity in each case. Next, we analyze the impact of commonly used assumptions, and as a further contribution, we propose a backpropagation algorithm for implementing the gradient descent method for a simplified SIM configuration.

Design of Reconfigurable Intelligent Surfaces by Using S-Parameter Multiport Network Theory -- Optimization and Full-Wave Validation

Multiport network theory has been proved to be a suitable abstraction model for analyzing and optimizing reconfigurable intelligent surfaces (RISs), especially for studying the impact of the electromagnetic mutual coupling among radiating elements that are spaced less than half of the wavelength. Both representations in terms of $Z$-parameter (impedance) and $S$-parameter (scattering) matrices are widely utilized. In this paper, we embrace multiport network theory for analyzing and optimizing the reradiation properties of RIS-aided channels, and provide four new contributions. (i) First, we offer a thorough comparison between the $Z$-parameter and $S$-parameter representations. This comparison allows us to unveil that the typical scattering models utilized for RIS-aided channels ignore the structural scattering from the RIS, which results in an unwanted specular reflection. (ii) Then, we develop an iterative algorithm for optimizing, in the presence of electromagnetic mutual coupling, the tunable loads of the RIS based on the $S$-parameters representation. We prove that small perturbations of the step size of the algorithm result in larger variations of the $S$-parameter matrix compared with the $Z$-parameter matrix, resulting in a faster convergence rate. (iii) Subsequently, we generalize the proposed algorithm to suppress the specular reflection due to the structural scattering, while maximizing the received power towards the direction of interest, and analyze the effectiveness and tradeoffs of the proposed approach. (iv) Finally, we validate the theoretical findings and algorithms with numerical simulations and a commercial full-wave electromagnetic simulator based on the method of moments.

Analysis and Optimization of Reconfigurable Intelligent Surfaces Based on $S$-Parameters Multiport Network Theory

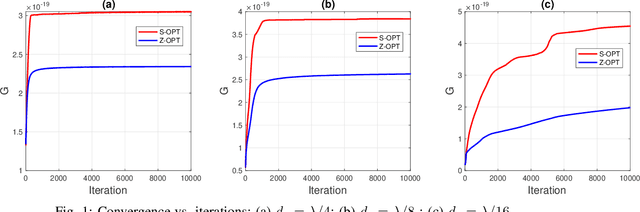
In this paper, we consider a reconfigurable intelligent surface (RIS) and model it by using multiport network theory. We first compare the representation of RIS by using $Z$-parameters and $S$-parameters, by proving their equivalence and discussing their distinct features. Then, we develop an algorithm for optimizing the RIS configuration in the presence of electromagnetic mutual coupling. We show that the proposed algorithm based on optimizing the $S$-parameters results in better performance than existing algorithms based on optimizing the $Z$-parameters. This is attributed to the fact that small perturbations of the step size of the proposed algorithm result in larger variations of the $S$-parameters, hence increasing the convergence speed of the algorithm.