MD-NOMAD: Mixture density nonlinear manifold decoder for emulating stochastic differential equations and uncertainty propagation

We propose a neural operator framework, termed mixture density nonlinear manifold decoder (MD-NOMAD), for stochastic simulators. Our approach leverages an amalgamation of the pointwise operator learning neural architecture nonlinear manifold decoder (NOMAD) with mixture density-based methods to estimate conditional probability distributions for stochastic output functions. MD-NOMAD harnesses the ability of probabilistic mixture models to estimate complex probability and the high-dimensional scalability of pointwise neural operator NOMAD. We conduct empirical assessments on a wide array of stochastic ordinary and partial differential equations and present the corresponding results, which highlight the performance of the proposed framework.

Multi-fidelity wavelet neural operator with application to uncertainty quantification

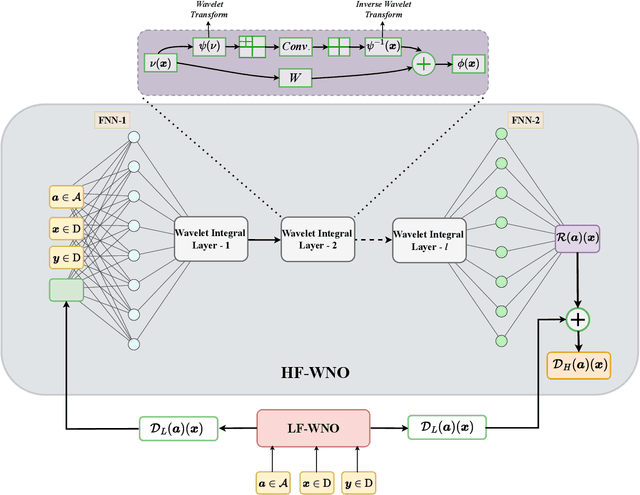
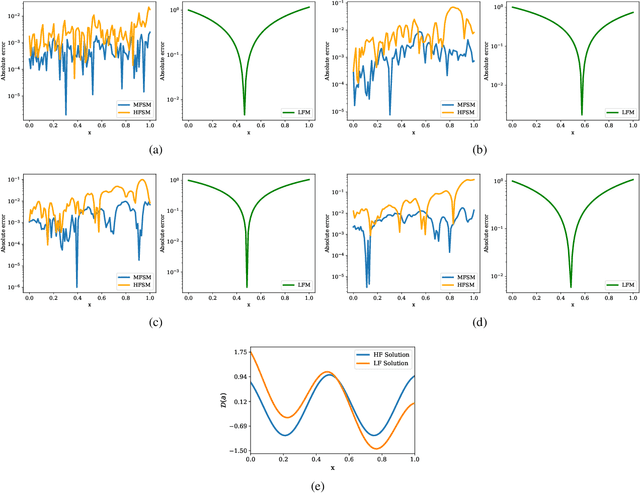
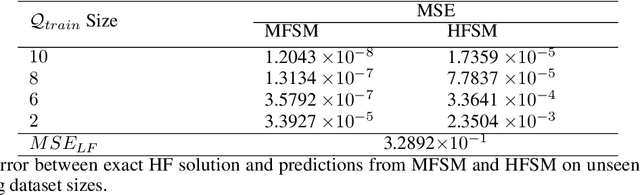
Operator learning frameworks, because of their ability to learn nonlinear maps between two infinite dimensional functional spaces and utilization of neural networks in doing so, have recently emerged as one of the more pertinent areas in the field of applied machine learning. Although these frameworks are extremely capable when it comes to modeling complex phenomena, they require an extensive amount of data for successful training which is often not available or is too expensive. However, this issue can be alleviated with the use of multi-fidelity learning, where a model is trained by making use of a large amount of inexpensive low-fidelity data along with a small amount of expensive high-fidelity data. To this end, we develop a new framework based on the wavelet neural operator which is capable of learning from a multi-fidelity dataset. The developed model's excellent learning capabilities are demonstrated by solving different problems which require effective correlation learning between the two fidelities for surrogate construction. Furthermore, we also assess the application of the developed framework for uncertainty quantification. The results obtained from this work illustrate the excellent performance of the proposed framework.

Deep Capsule Encoder-Decoder Network for Surrogate Modeling and Uncertainty Quantification

We propose a novel \textit{capsule} based deep encoder-decoder model for surrogate modeling and uncertainty quantification of systems in mechanics from sparse data. The proposed framework is developed by adapting Capsule Network (CapsNet) architecture into image-to-image regression encoder-decoder network. Specifically, the aim is to exploit the benefits of CapsNet over convolution neural network (CNN) $-$ retaining pose and position information related to an entity to name a few. The performance of proposed approach is illustrated by solving an elliptic stochastic partial differential equation (SPDE), which also governs systems in mechanics such as steady heat conduction, ground water flow or other diffusion processes, based uncertainty quantification problem with an input dimensionality of $1024$. However, the problem definition does not the restrict the random diffusion field to a particular covariance structure, and the more strenuous task of response prediction for an arbitrary diffusion field is solved. The obtained results from performance evaluation indicate that the proposed approach is accurate, efficient, and robust.

A deep learning based surrogate model for stochastic simulators

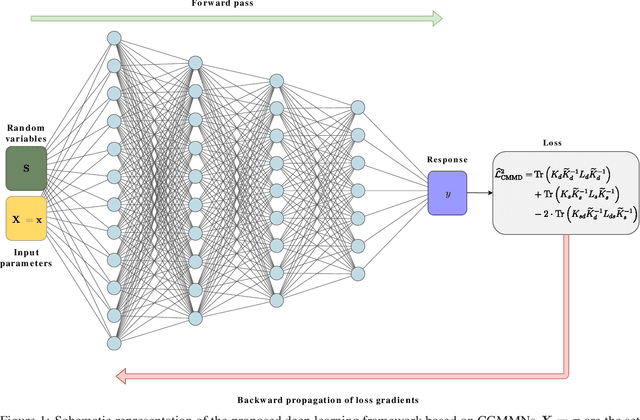
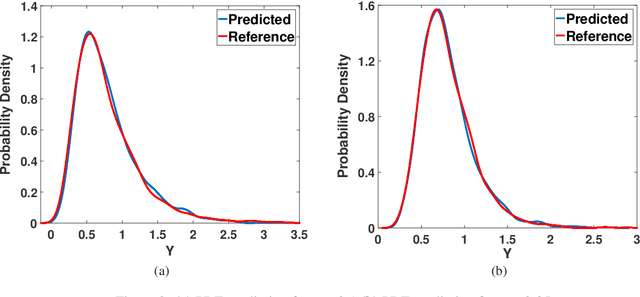
We propose a deep learning-based surrogate model for stochastic simulators. The basic idea is to use generative neural network to approximate the stochastic response. The challenge with such a framework resides in designing the network architecture and selecting loss-function suitable for stochastic response. While we utilize a simple feed-forward neural network, we propose to use conditional maximum mean discrepancy (CMMD) as the loss-function. CMMD exploits the property of reproducing kernel Hilbert space and allows capturing discrepancy between the between the target and the neural network predicted distributions. The proposed approach is mathematically rigorous, in the sense that it makes no assumptions about the probability density function of the response. Performance of the proposed approach is illustrated using four benchmark problems selected from the literature. Results obtained indicate the excellent performance of the proposed approach.