Ailisi Li
Tackling Math Word Problems with Fine-to-Coarse Abstracting and Reasoning
May 17, 2022
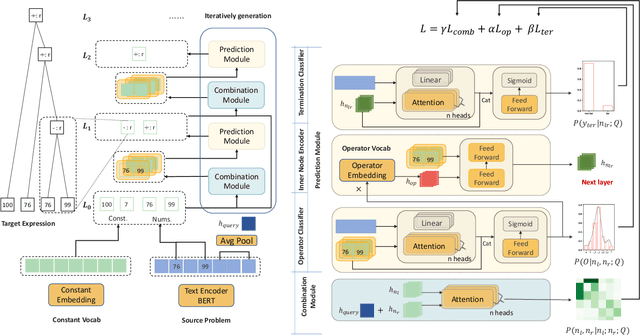
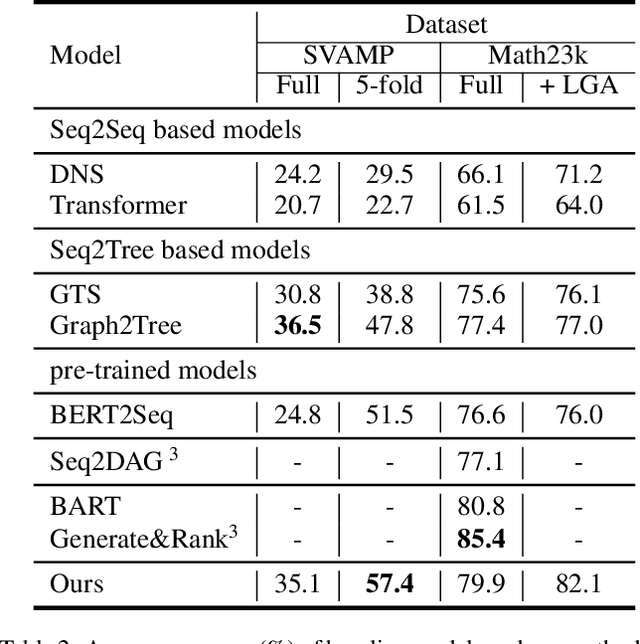
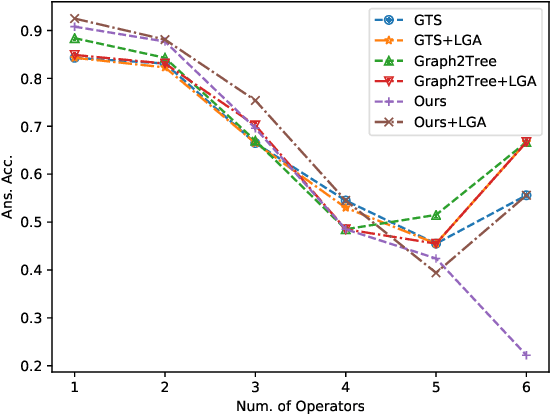
Abstract:Math Word Problems (MWP) is an important task that requires the ability of understanding and reasoning over mathematical text. Existing approaches mostly formalize it as a generation task by adopting Seq2Seq or Seq2Tree models to encode an input math problem in natural language as a global representation and generate the output mathematical expression. Such approaches only learn shallow heuristics and fail to capture fine-grained variations in inputs. In this paper, we propose to model a math word problem in a fine-to-coarse manner to capture both the local fine-grained information and the global logical structure of it. Instead of generating a complete equation sequence or expression tree from the global features, we iteratively combine low-level operands to predict a higher-level operator, abstracting the problem and reasoning about the solving operators from bottom to up. Our model is naturally more sensitive to local variations and can better generalize to unseen problem types. Extensive evaluations on Math23k and SVAMP datasets demonstrate the accuracy and robustness of our method.
Semantic-based Data Augmentation for Math Word Problems
Jan 07, 2022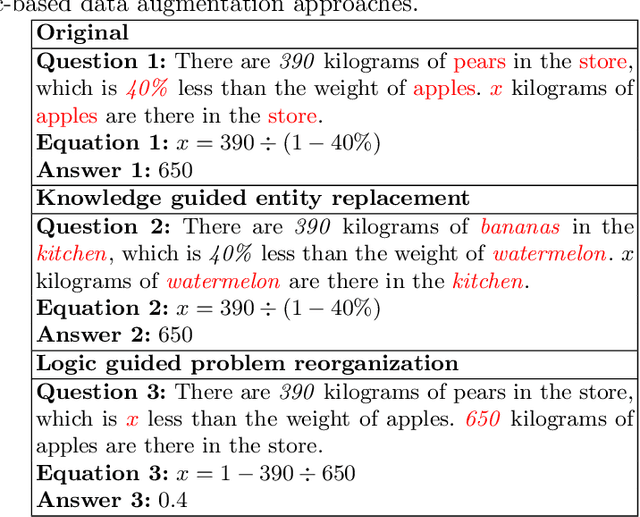
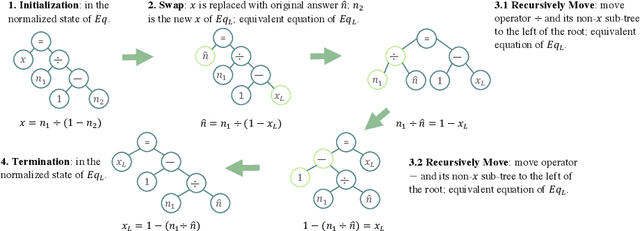
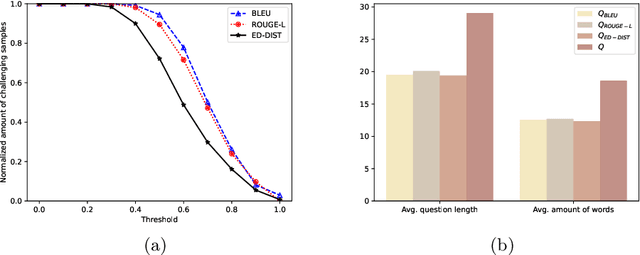

Abstract:It's hard for neural MWP solvers to deal with tiny local variances. In MWP task, some local changes conserve the original semantic while the others may totally change the underlying logic. Currently, existing datasets for MWP task contain limited samples which are key for neural models to learn to disambiguate different kinds of local variances in questions and solve the questions correctly. In this paper, we propose a set of novel data augmentation approaches to supplement existing datasets with such data that are augmented with different kinds of local variances, and help to improve the generalization ability of current neural models. New samples are generated by knowledge guided entity replacement, and logic guided problem reorganization. The augmentation approaches are ensured to keep the consistency between the new data and their labels. Experimental results have shown the necessity and the effectiveness of our methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge