Aigerim Zhuman
Sliced-Wasserstein Estimation with Spherical Harmonics as Control Variates
Feb 02, 2024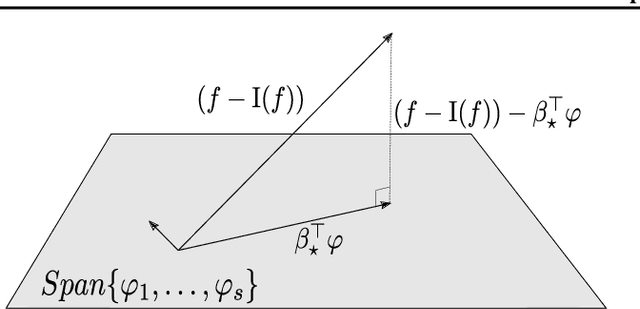
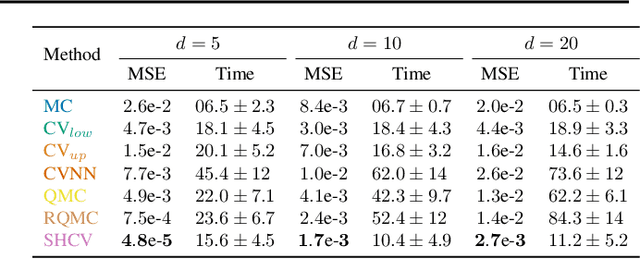
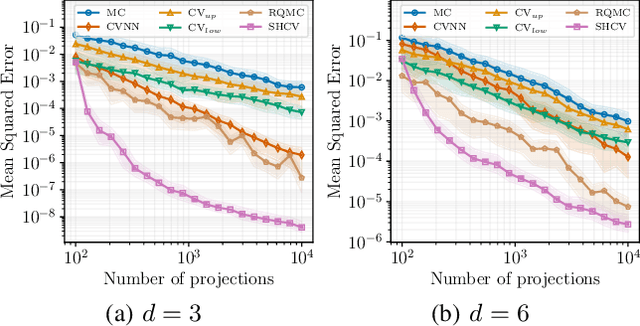

Abstract:The Sliced-Wasserstein (SW) distance between probability measures is defined as the average of the Wasserstein distances resulting for the associated one-dimensional projections. As a consequence, the SW distance can be written as an integral with respect to the uniform measure on the sphere and the Monte Carlo framework can be employed for calculating the SW distance. Spherical harmonics are polynomials on the sphere that form an orthonormal basis of the set of square-integrable functions on the sphere. Putting these two facts together, a new Monte Carlo method, hereby referred to as Spherical Harmonics Control Variates (SHCV), is proposed for approximating the SW distance using spherical harmonics as control variates. The resulting approach is shown to have good theoretical properties, e.g., a no-error property for Gaussian measures under a certain form of linear dependency between the variables. Moreover, an improved rate of convergence, compared to Monte Carlo, is established for general measures. The convergence analysis relies on the Lipschitz property associated to the SW integrand. Several numerical experiments demonstrate the superior performance of SHCV against state-of-the-art methods for SW distance computation.
A Quadrature Rule combining Control Variates and Adaptive Importance Sampling
May 24, 2022
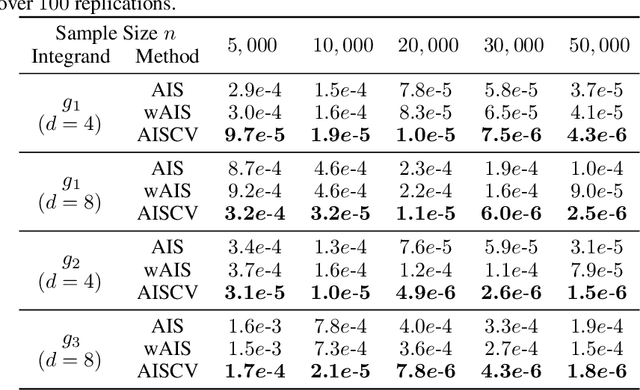
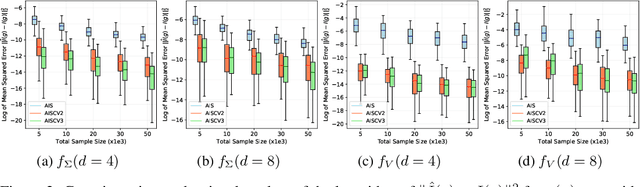
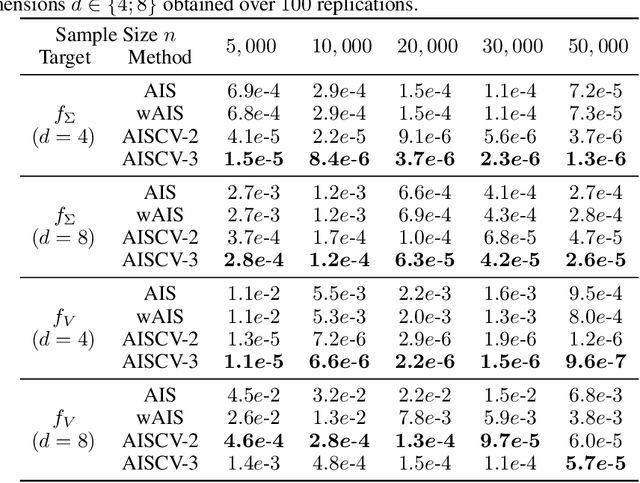
Abstract:Driven by several successful applications such as in stochastic gradient descent or in Bayesian computation, control variates have become a major tool for Monte Carlo integration. However, standard methods do not allow the distribution of the particles to evolve during the algorithm, as is the case in sequential simulation methods. Within the standard adaptive importance sampling framework, a simple weighted least squares approach is proposed to improve the procedure with control variates. The procedure takes the form of a quadrature rule with adapted quadrature weights to reflect the information brought in by the control variates. The quadrature points and weights do not depend on the integrand, a computational advantage in case of multiple integrands. Moreover, the target density needs to be known only up to a multiplicative constant. Our main result is a non-asymptotic bound on the probabilistic error of the procedure. The bound proves that for improving the estimate's accuracy, the benefits from adaptive importance sampling and control variates can be combined. The good behavior of the method is illustrated empirically on synthetic examples and real-world data for Bayesian linear regression.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge