A Quadrature Rule combining Control Variates and Adaptive Importance Sampling
Paper and Code
May 24, 2022
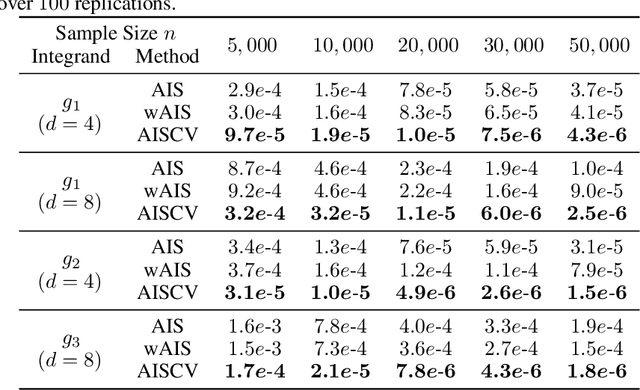
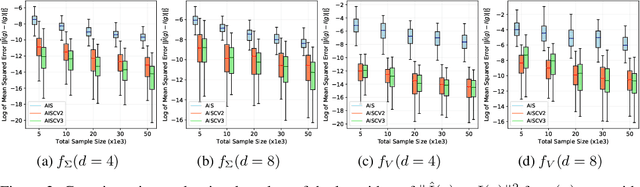
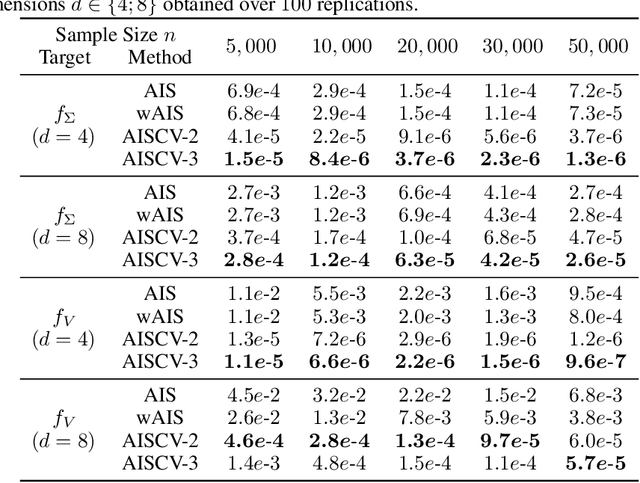
Driven by several successful applications such as in stochastic gradient descent or in Bayesian computation, control variates have become a major tool for Monte Carlo integration. However, standard methods do not allow the distribution of the particles to evolve during the algorithm, as is the case in sequential simulation methods. Within the standard adaptive importance sampling framework, a simple weighted least squares approach is proposed to improve the procedure with control variates. The procedure takes the form of a quadrature rule with adapted quadrature weights to reflect the information brought in by the control variates. The quadrature points and weights do not depend on the integrand, a computational advantage in case of multiple integrands. Moreover, the target density needs to be known only up to a multiplicative constant. Our main result is a non-asymptotic bound on the probabilistic error of the procedure. The bound proves that for improving the estimate's accuracy, the benefits from adaptive importance sampling and control variates can be combined. The good behavior of the method is illustrated empirically on synthetic examples and real-world data for Bayesian linear regression.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge