Ahmet Satir
A Scheme for Dynamic Risk-Sensitive Sequential Decision Making
Jul 09, 2019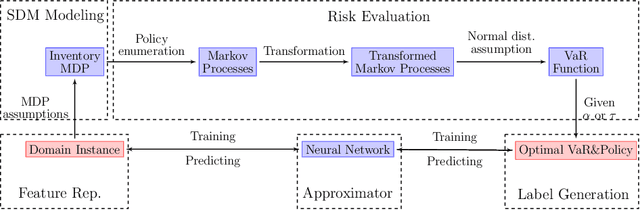


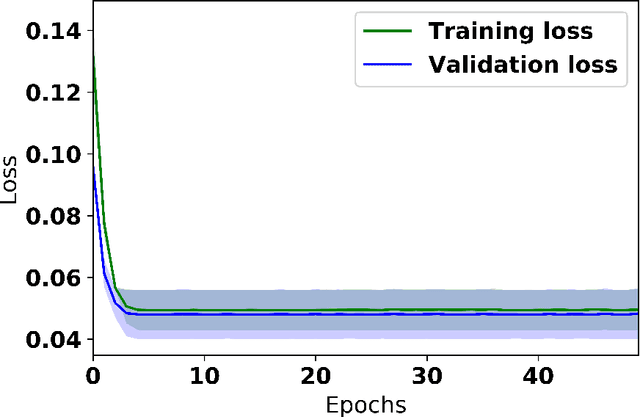
Abstract:We present a scheme for sequential decision making with a risk-sensitive objective and constraints in a dynamic environment. A neural network is trained as an approximator of the mapping from parameter space to space of risk and policy with risk-sensitive constraints. For a given risk-sensitive problem, in which the objective and constraints are, or can be estimated by, functions of the mean and variance of return, we generate a synthetic dataset as training data. Parameters defining a targeted process might be dynamic, i.e., they might vary over time, so we sample them within specified intervals to deal with these dynamics. We show that: i). Most risk measures can be estimated using return variance; ii). By virtue of the state-augmentation transformation, practical problems modeled by Markov decision processes with stochastic rewards can be solved in a risk-sensitive scenario; and iii). The proposed scheme is validated by a numerical experiment.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge