KHNNs: hypercomplex neural networks computations via Keras using TensorFlow and PyTorch

Neural networks used in computations with more advanced algebras than real numbers perform better in some applications. However, there is no general framework for constructing hypercomplex neural networks. We propose a library integrated with Keras that can do computations within TensorFlow and PyTorch. It provides Dense and Convolutional 1D, 2D, and 3D layers architectures.

Fully tensorial approach to hypercomplex neural networks

Fully tensorial theory of hypercomplex neural networks is given. The key point is to observe that the algebra multiplication can be represented as a rank three tensor. This approach is attractive for neural network libraries that support effective tensorial operations.

A Critical Analysis of the Theoretical Framework of the Extreme Learning Machine

Despite the number of successful applications of the Extreme Learning Machine (ELM), we show that its underlying foundational principles do not have a rigorous mathematical justification. Specifically, we refute the proofs of two main statements, and we also create a dataset that provides a counterexample to the ELM learning algorithm and explain its design, which leads to many such counterexamples. Finally, we provide alternative statements of the foundations, which justify the efficiency of ELM in some theoretical cases.

Hypercomplex neural network in time series forecasting of stock data

The three classes of architectures for time series prediction were tested. They differ by input layers which contain either convolutional, LSTM, or dense hypercomplex layers for 4D algebras. The input was four related Stock Market time series, and the prediction of one of them is expected. The optimization of hyperparameters related to the classes of architectures was performed in order to compare the best neural networks within the class. The results show that in most cases, the architecture with a hypercomplex dense layer provides similar MAE accuracy to other architectures, however, with considerably less trainable parameters. Thanks to it, hypercomplex neural networks can be learned and process data faster than the other tested architectures. Moreover, the order of the input time series has an impact on effectively.

Selected aspects of complex, hypercomplex and fuzzy neural networks

This short report reviews the current state of the research and methodology on theoretical and practical aspects of Artificial Neural Networks (ANN). It was prepared to gather state-of-the-art knowledge needed to construct complex, hypercomplex and fuzzy neural networks. The report reflects the individual interests of the authors and, by now means, cannot be treated as a comprehensive review of the ANN discipline. Considering the fast development of this field, it is currently impossible to do a detailed review of a considerable number of pages. The report is an outcome of the Project 'The Strategic Research Partnership for the mathematical aspects of complex, hypercomplex and fuzzy neural networks' meeting at the University of Warmia and Mazury in Olsztyn, Poland, organized in September 2022.

Stimulation of soy seeds using environmentally friendly magnetic and electric fields

The study analyzes the impact of constant and alternating magnetic fields and alternating electric fields on various growth parameters of soy plants: the germination energy and capacity, plants emergence and number, the Yield(II) of the fresh mass of seedlings, protein content, and photosynthetic parameters. Four cultivars were used: MAVKA, MERLIN, VIOLETTA, and ANUSZKA. Moreover, the advanced Machine Learning processing pipeline was proposed to distinguish the impact of physical factors on photosynthetic parameters. It is possible to distinguish exposition on different physical factors for the first three cultivars; therefore, it indicates that the EM factors have some observable effect on soy plants. Moreover, some influence of physical factors on growth parameters was observed. The use of ELM (Electromagnetic) fields had a positive impact on the germination rate in Merlin plants. The highest values were recorded for the constant magnetic field (CMF) - Merlin, and the lowest for the alternating electric field (AEF) - Violetta. An increase in terms of emergence and number of plants after seed stimulation was observed for the Mavka cultivar, except for the AEF treatment (number of plants after 30 days) (...)

Towards the global vision of engagement of Generation Z at the workplace: Mathematical modeling

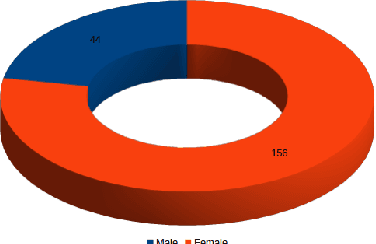
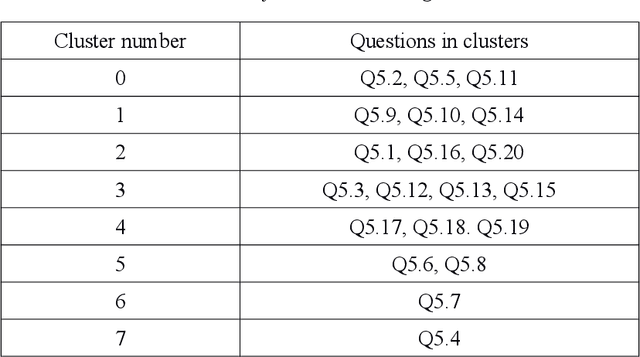
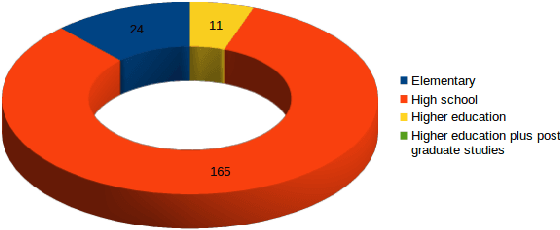
Correlation and cluster analyses (k-Means, Gaussian Mixture Models) were performed on Generation Z engagement surveys at the workplace. The clustering indicates relations between various factors that describe the engagement of employees. The most noticeable factors are a clear statement about the responsibilities at work, and challenging work. These factors are essential in practice. The results of this paper can be used in preparing better motivational systems aimed at Generation Z employees.

TreeGen -- a Monte Carlo generator for data frames

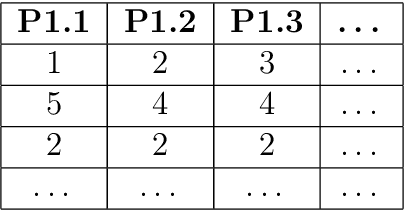
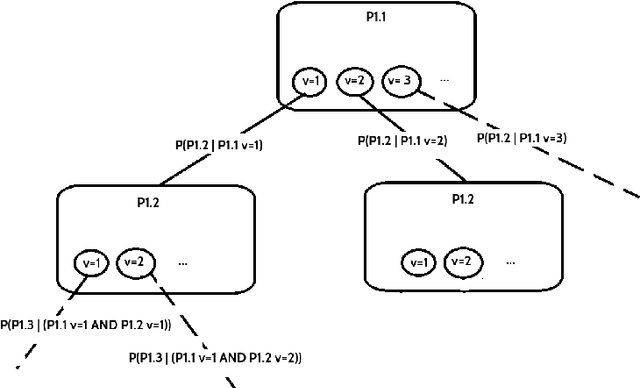
The typical problem in Data Science is creating a structure that encodes the occurrence frequency of unique elements in rows and relations between different rows of a data frame. We present the probability tree abstract data structure, an extension of the decision tree, that facilitates more than two choices with assigned probabilities. Such a tree represents statistical relations between different rows of the data frame. The Probability Tree algorithmic structure is supplied with the Generator module that is a Monte Carlo generator that traverses through the tree. These two components are implemented in TreeGen Python package. The package can be used in increasing data multiplicity, compressing data preserving its statistical information, constructing hierarchical models, exploring data, and in feature extraction.