Afonso Fernandes Vaz
Quantification under prior probability shift: the ratio estimator and its extensions
Jul 11, 2018
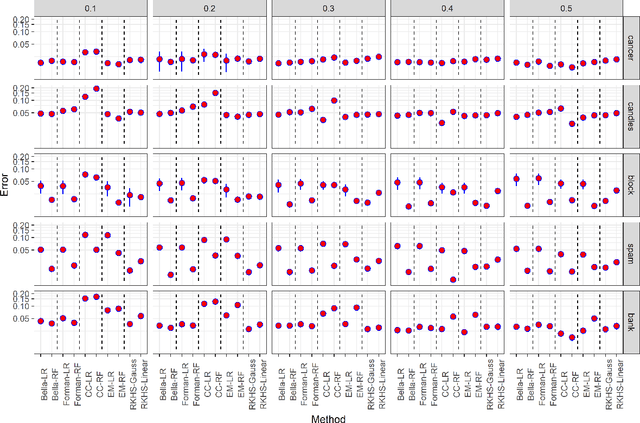
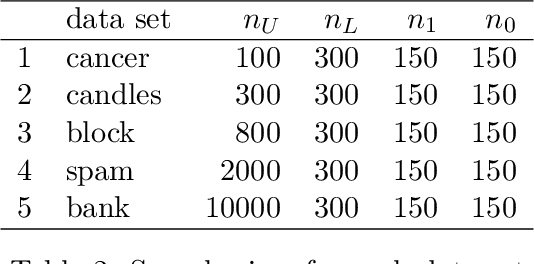
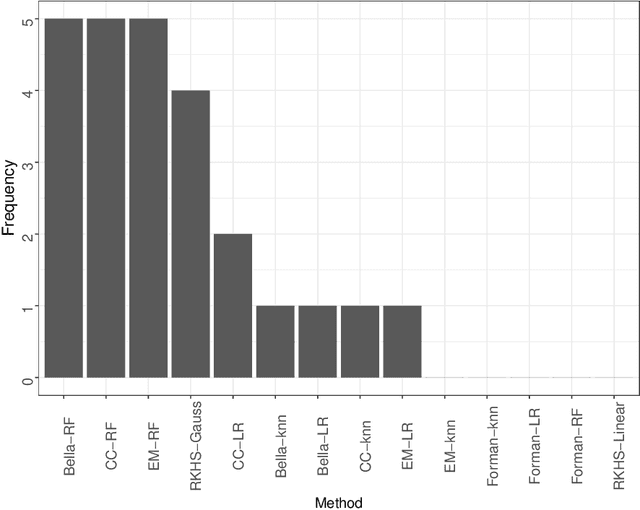
Abstract:The quantification problem consists of determining the prevalence of a given label in a target population. However, one often has access to the labels in a sample from the training population but not in the target population. A common assumption in this situation is that of prior probability shift, that is, once the labels are known, the distribution of the features is the same in the training and target populations. In this paper, we derive a new lower bound for the risk of the quantification problem under the prior shift assumption. Complementing this lower bound, we present a new approximately minimax class of estimators, ratio estimators, which generalize several previous proposals in the literature. Using a weaker version of the prior shift assumption, which can be tested, we show that ratio estimators can be used to build confidence intervals for the quantification problem. We also extend the ratio estimator so that it can: (i) incorporate labels from the target population, when they are available and (ii) estimate how the prevalence of positive labels varies according to a function of certain covariates.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge