Adrien Lagrange
Matrix cofactorization for joint spatial-spectral unmixing of hyperspectral images
Jul 19, 2019



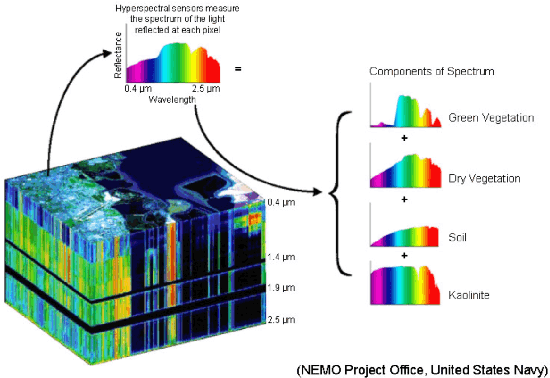
Abstract:Hyperspectral unmixing aims at identifying a set of elementary spectra and the corresponding mixture coefficients for each pixel of an image. As the elementary spectra correspond to the reflectance spectra of real materials, they are often very correlated yielding an ill-conditioned problem. To enrich the model and to reduce ambiguity due to the high correlation, it is common to introduce spatial information to complement the spectral information. The most common way to introduce spatial information is to rely on a spatial regularization of the abundance maps. In this paper, instead of considering a simple but limited regularization process, spatial information is directly incorporated through the newly proposed context of spatial unmixing. Contextual features are extracted for each pixel and this additional set of observations is decomposed according to a linear model. Finally the spatial and spectral observations are unmixed jointly through a cofactorization model. In particular, this model introduces a coupling term used to identify clusters of shared spatial and spectral signatures. An evaluation of the proposed method is conducted on synthetic and real data and shows that results are accurate and also very meaningful since they describe both spatially and spectrally the various areas of the scene.
Matrix Cofactorization for Joint Representation Learning and Supervised Classification -- Application to Hyperspectral Image Analysis
Feb 07, 2019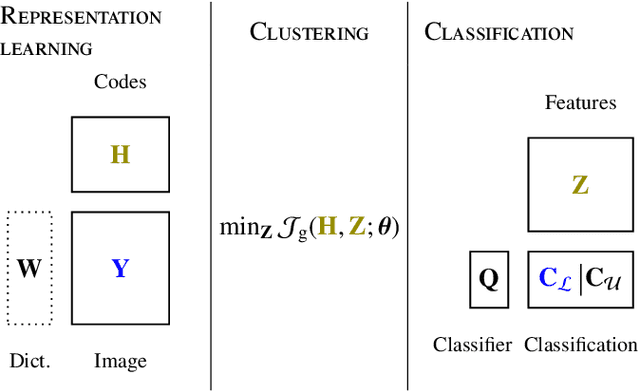
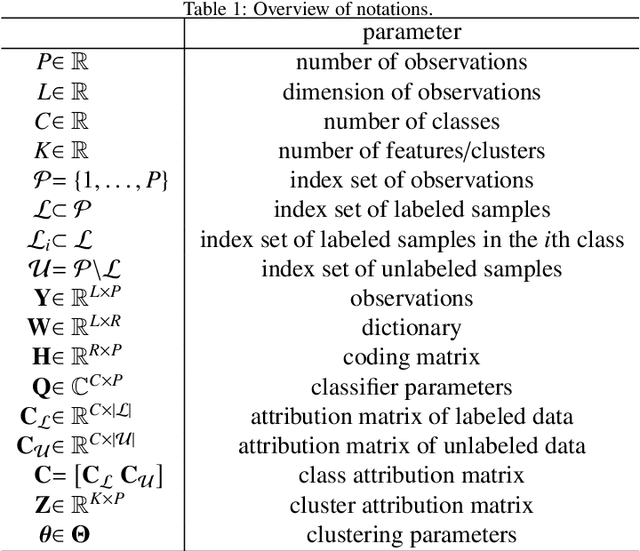

Abstract:Supervised classification and representation learning are two widely used methods to analyze multivariate images. Although complementary, these two classes of methods have been scarcely considered jointly. In this paper, a method coupling these two approaches is designed using a matrix cofactorization formulation. Each task is modeled as a factorization matrix problem and a term relating both coding matrices is then introduced to drive an appropriate coupling. The link can be interpreted as a clustering operation over the low-dimensional representation vectors. The attribution vectors of the clustering are then used as features vectors for the classification task, i.e., the coding vectors of the corresponding factorization problem. A proximal gradient descent algorithm, ensuring convergence to a critical point of the objective function, is then derived to solve the resulting non-convex non-smooth optimization problem. An evaluation of the proposed method is finally conducted both on synthetic and real data in the specific context of hyperspectral image interpretation, unifying two standard analysis techniques, namely unmixing and classification.
Hierarchical Bayesian image analysis: from low-level modeling to robust supervised learning
Dec 01, 2017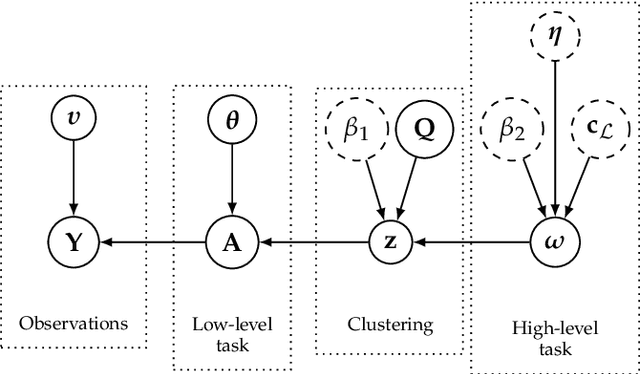
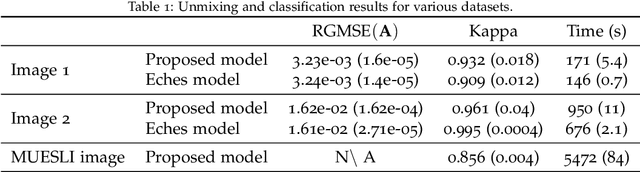

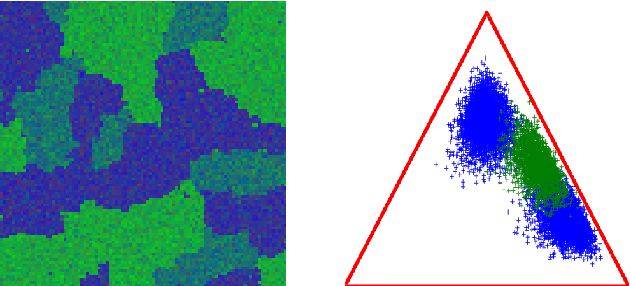
Abstract:Within a supervised classification framework, labeled data are used to learn classifier parameters. Prior to that, it is generally required to perform dimensionality reduction via feature extraction. These preprocessing steps have motivated numerous research works aiming at recovering latent variables in an unsupervised context. This paper proposes a unified framework to perform classification and low-level modeling jointly. The main objective is to use the estimated latent variables as features for classification and to incorporate simultaneously supervised information to help latent variable extraction. The proposed hierarchical Bayesian model is divided into three stages: a first low-level modeling stage to estimate latent variables, a second stage clustering these features into statistically homogeneous groups and a last classification stage exploiting the (possibly badly) labeled data. Performance of the model is assessed in the specific context of hyperspectral image interpretation, unifying two standard analysis techniques, namely unmixing and classification.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge