A New Interpretable Neural Network-Based Rule Model for Healthcare Decision Making

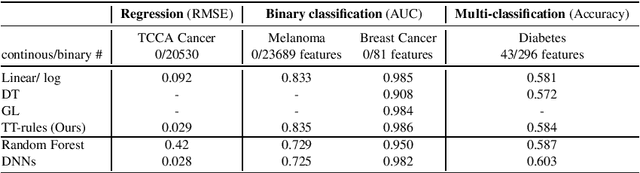
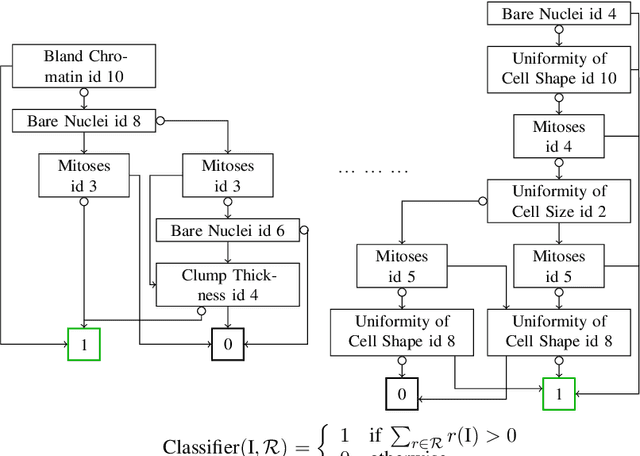
In healthcare applications, understanding how machine/deep learning models make decisions is crucial. In this study, we introduce a neural network framework, $\textit{Truth Table rules}$ (TT-rules), that combines the global and exact interpretability properties of rule-based models with the high performance of deep neural networks. TT-rules is built upon $\textit{Truth Table nets}$ (TTnet), a family of deep neural networks initially developed for formal verification. By extracting the necessary and sufficient rules $\mathcal{R}$ from the trained TTnet model (global interpretability) to yield the same output as the TTnet (exact interpretability), TT-rules effectively transforms the neural network into a rule-based model. This rule-based model supports binary classification, multi-label classification, and regression tasks for small to large tabular datasets. After outlining the framework, we evaluate TT-rules' performance on healthcare applications and compare it to state-of-the-art rule-based methods. Our results demonstrate that TT-rules achieves equal or higher performance compared to other interpretable methods. Notably, TT-rules presents the first accurate rule-based model capable of fitting large tabular datasets, including two real-life DNA datasets with over 20K features.

Neural Network-Based Rule Models With Truth Tables

Understanding the decision-making process of a machine/deep learning model is crucial, particularly in security-sensitive applications. In this study, we introduce a neural network framework that combines the global and exact interpretability properties of rule-based models with the high performance of deep neural networks. Our proposed framework, called $\textit{Truth Table rules}$ (TT-rules), is built upon $\textit{Truth Table nets}$ (TTnets), a family of deep neural networks initially developed for formal verification. By extracting the set of necessary and sufficient rules $\mathcal{R}$ from the trained TTnet model (global interpretability), yielding the same output as the TTnet (exact interpretability), TT-rules effectively transforms the neural network into a rule-based model. This rule-based model supports binary classification, multi-label classification, and regression tasks for tabular datasets. Furthermore, our TT-rules framework optimizes the rule set $\mathcal{R}$ into $\mathcal{R}_{opt}$ by reducing the number and size of the rules. To enhance model interpretation, we leverage Reduced Ordered Binary Decision Diagrams (ROBDDs) to visualize these rules effectively. After outlining the framework, we evaluate the performance of TT-rules on seven tabular datasets from finance, healthcare, and justice domains. We also compare the TT-rules framework to state-of-the-art rule-based methods. Our results demonstrate that TT-rules achieves equal or higher performance compared to other interpretable methods while maintaining a balance between performance and complexity. Notably, TT-rules presents the first accurate rule-based model capable of fitting large tabular datasets, including two real-life DNA datasets with over 20K features. Finally, we extensively investigate a rule-based model derived from TT-rules using the Adult dataset.

TT-TFHE: a Torus Fully Homomorphic Encryption-Friendly Neural Network Architecture

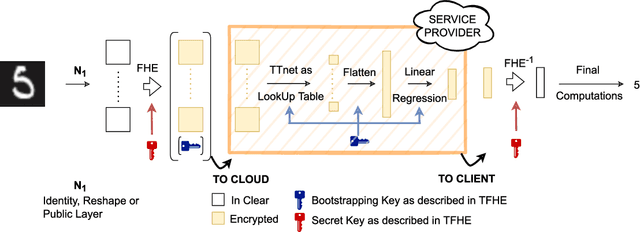
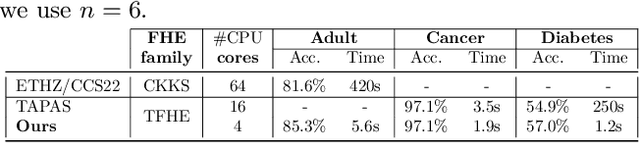
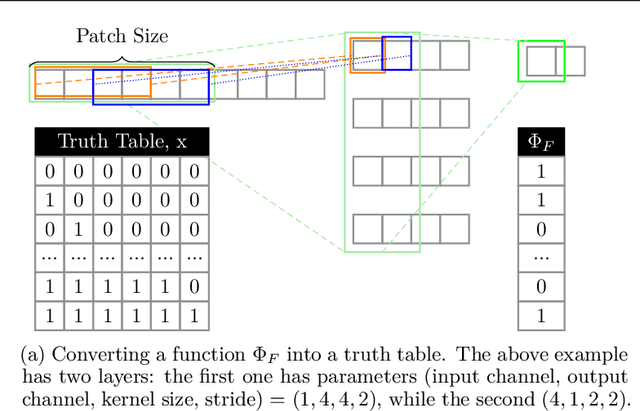
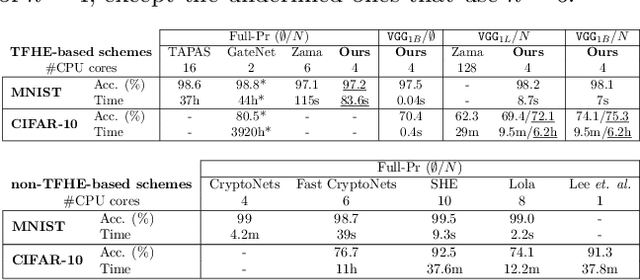
This paper presents TT-TFHE, a deep neural network Fully Homomorphic Encryption (FHE) framework that effectively scales Torus FHE (TFHE) usage to tabular and image datasets using a recent family of convolutional neural networks called Truth-Table Neural Networks (TTnet). The proposed framework provides an easy-to-implement, automated TTnet-based design toolbox with an underlying (python-based) open-source Concrete implementation (CPU-based and implementing lookup tables) for inference over encrypted data. Experimental evaluation shows that TT-TFHE greatly outperforms in terms of time and accuracy all Homomorphic Encryption (HE) set-ups on three tabular datasets, all other features being equal. On image datasets such as MNIST and CIFAR-10, we show that TT-TFHE consistently and largely outperforms other TFHE set-ups and is competitive against other HE variants such as BFV or CKKS (while maintaining the same level of 128-bit encryption security guarantees). In addition, our solutions present a very low memory footprint (down to dozens of MBs for MNIST), which is in sharp contrast with other HE set-ups that typically require tens to hundreds of GBs of memory per user (in addition to their communication overheads). This is the first work presenting a fully practical solution of private inference (i.e. a few seconds for inference time and a few dozens MBs of memory) on both tabular datasets and MNIST, that can easily scale to multiple threads and users on server side.

Truth-Table Net: A New Convolutional Architecture Encodable By Design Into SAT Formulas

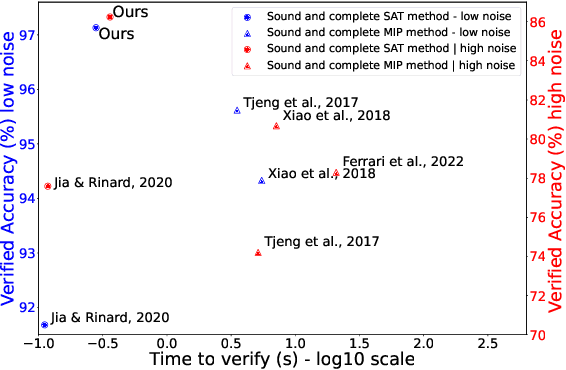
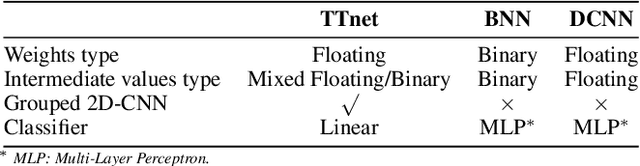
With the expanding role of neural networks, the need for complete and sound verification of their property has become critical. In the recent years, it was established that Binary Neural Networks (BNNs) have an equivalent representation in Boolean logic and can be formally analyzed using logical reasoning tools such as SAT solvers. However, to date, only BNNs can be transformed into a SAT formula. In this work, we introduce Truth Table Deep Convolutional Neural Networks (TTnets), a new family of SAT-encodable models featuring for the first time real-valued weights. Furthermore, it admits, by construction, some valuable conversion features including post-tuning and tractability in the robustness verification setting. The latter property leads to a more compact SAT symbolic encoding than BNNs. This enables the use of general SAT solvers, making property verification easier. We demonstrate the value of TTnets regarding the formal robustness property: TTnets outperform the verified accuracy of all BNNs with a comparable computation time. More generally, they represent a relevant trade-off between all known complete verification methods: TTnets achieve high verified accuracy with fast verification time, being complete with no timeouts. We are exploring here a proof of concept of TTnets for a very important application (complete verification of robustness) and we believe this novel real-valued network constitutes a practical response to the rising need for functional formal verification. We postulate that TTnets can apply to various CNN-based architectures and be extended to other properties such as fairness, fault attack and exact rule extraction.