Bryan Hooi Kuen-Yew
Truth-Table Net: A New Convolutional Architecture Encodable By Design Into SAT Formulas
Aug 18, 2022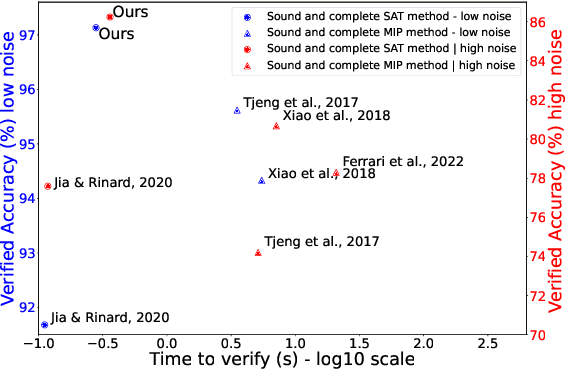


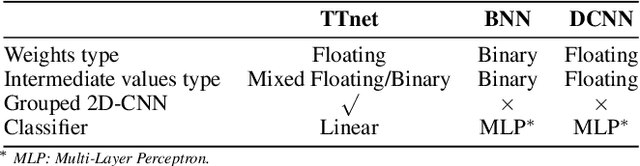
Abstract:With the expanding role of neural networks, the need for complete and sound verification of their property has become critical. In the recent years, it was established that Binary Neural Networks (BNNs) have an equivalent representation in Boolean logic and can be formally analyzed using logical reasoning tools such as SAT solvers. However, to date, only BNNs can be transformed into a SAT formula. In this work, we introduce Truth Table Deep Convolutional Neural Networks (TTnets), a new family of SAT-encodable models featuring for the first time real-valued weights. Furthermore, it admits, by construction, some valuable conversion features including post-tuning and tractability in the robustness verification setting. The latter property leads to a more compact SAT symbolic encoding than BNNs. This enables the use of general SAT solvers, making property verification easier. We demonstrate the value of TTnets regarding the formal robustness property: TTnets outperform the verified accuracy of all BNNs with a comparable computation time. More generally, they represent a relevant trade-off between all known complete verification methods: TTnets achieve high verified accuracy with fast verification time, being complete with no timeouts. We are exploring here a proof of concept of TTnets for a very important application (complete verification of robustness) and we believe this novel real-valued network constitutes a practical response to the rising need for functional formal verification. We postulate that TTnets can apply to various CNN-based architectures and be extended to other properties such as fairness, fault attack and exact rule extraction.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge