Adrian Vetta
Gerrymandering Planar Graphs
Jan 08, 2024Abstract:We study the computational complexity of the map redistricting problem (gerrymandering). Mathematically, the electoral district designer (gerrymanderer) attempts to partition a weighted graph into $k$ connected components (districts) such that its candidate (party) wins as many districts as possible. Prior work has principally concerned the special cases where the graph is a path or a tree. Our focus concerns the realistic case where the graph is planar. We prove that the gerrymandering problem is solvable in polynomial time in $\lambda$-outerplanar graphs, when the number of candidates and $\lambda$ are constants and the vertex weights (voting weights) are polynomially bounded. In contrast, the problem is NP-complete in general planar graphs even with just two candidates. This motivates the study of approximation algorithms for gerrymandering planar graphs. However, when the number of candidates is large, we prove it is hard to distinguish between instances where the gerrymanderer cannot win a single district and instances where the gerrymanderer can win at least one district. This immediately implies that the redistricting problem is inapproximable in polynomial time in planar graphs, unless P=NP. This conclusion appears terminal for the design of good approximation algorithms -- but it is not. The inapproximability bound can be circumvented as it only applies when the maximum number of districts the gerrymanderer can win is extremely small, say one. Indeed, for a fixed number of candidates, our main result is that there is a constant factor approximation algorithm for redistricting unweighted planar graphs, provided the optimal value is a large enough constant.
Penalties and Rewards for Fair Learning in Paired Kidney Exchange Programs
Sep 23, 2023Abstract:A kidney exchange program, also called a kidney paired donation program, can be viewed as a repeated, dynamic trading and allocation mechanism. This suggests that a dynamic algorithm for transplant exchange selection may have superior performance in comparison to the repeated use of a static algorithm. We confirm this hypothesis using a full scale simulation of the Canadian Kidney Paired Donation Program: learning algorithms, that attempt to learn optimal patient-donor weights in advance via dynamic simulations, do lead to improved outcomes. Specifically, our learning algorithms, designed with the objective of fairness (that is, equity in terms of transplant accessibility across cPRA groups), also lead to an increased number of transplants and shorter average waiting times. Indeed, our highest performing learning algorithm improves egalitarian fairness by 10% whilst also increasing the number of transplants by 6% and decreasing waiting times by 24%. However, our main result is much more surprising. We find that the most critical factor in determining the performance of a kidney exchange program is not the judicious assignment of positive weights (rewards) to patient-donor pairs. Rather, the key factor in increasing the number of transplants, decreasing waiting times and improving group fairness is the judicious assignment of a negative weight (penalty) to the small number of non-directed donors in the kidney exchange program.
Fair Algorithm Design: Fair and Efficacious Machine Scheduling
Apr 13, 2022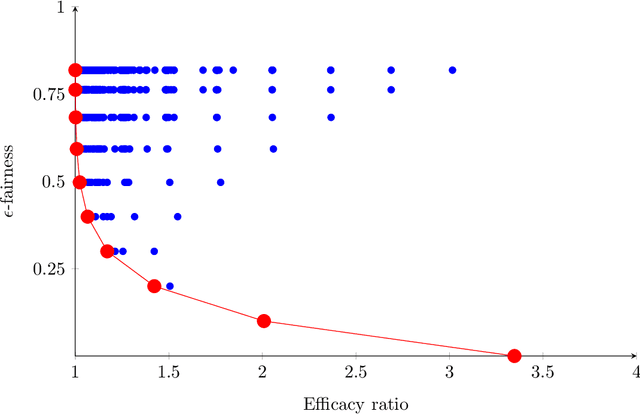
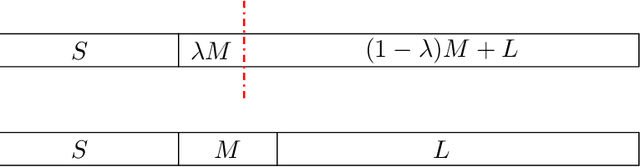

Abstract:Motivated by a plethora of practical examples where bias is induced by automated-decision making algorithms, there has been strong recent interest in the design of fair algorithms. However, there is often a dichotomy between fairness and efficacy: fair algorithms may proffer low social welfare solutions whereas welfare optimizing algorithms may be very unfair. This issue is exemplified in the machine scheduling problem where, for $n$ jobs, the social welfare of any fair solution may be a factor $\Omega(n)$ worse than the optimal welfare. In this paper, we prove that this dichotomy between fairness and efficacy can be overcome if we allow for a negligible amount of bias: there exist algorithms that are both "almost perfectly fair" and have a constant factor efficacy ratio, that is, are guaranteed to output solutions that have social welfare within a constant factor of optimal welfare. Specifically, for any $\epsilon>0$, there exist mechanisms with efficacy ratio $\Theta(\frac{1}{\epsilon})$ and where no agent is more than an $\epsilon$ fraction worse off than they are in the fairest possible solution (given by an algorithm that does not use personal or type data). Moreover, these bicriteria guarantees are tight and apply to both the single machine case and the multiple machine case. The key to our results are the use of Pareto scheduling mechanisms. These mechanisms, by the judicious use of personal or type data, are able to exploit Pareto improvements that benefit every individual; such Pareto improvements would typically be forbidden by fair scheduling algorithms designed to satisfy standard statistical measures of group fairness. We anticipate this paradigm, the judicious use of personal data by a fair algorithm to greatly improve performance at the cost of negligible bias, has wider application.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge