Adrian Haret
An AGM Approach to Revising Preferences
Dec 28, 2021



Abstract:We look at preference change arising out of an interaction between two elements: the first is an initial preference ranking encoding a pre-existing attitude; the second element is new preference information signaling input from an authoritative source, which may come into conflict with the initial preference. The aim is to adjust the initial preference and bring it in line with the new preference, without having to give up more information than necessary. We model this process using the formal machinery of belief change, along the lines of the well-known AGM approach. We propose a set of fundamental rationality postulates, and derive the main results of the paper: a set of representation theorems showing that preference change according to these postulates can be rationalized as a choice function guided by a ranking on the comparisons in the initial preference order. We conclude by presenting operators satisfying our proposed postulates. Our approach thus allows us to situate preference revision within the larger family of belief change operators.
Surprise Minimization Revision Operators
Nov 21, 2021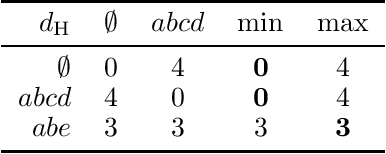
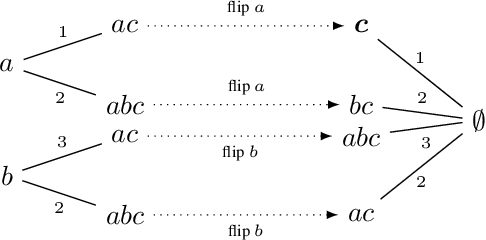

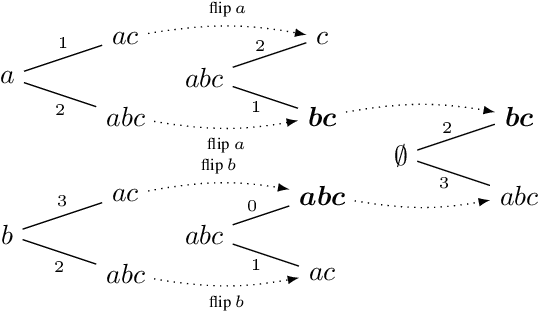
Abstract:Prominent approaches to belief revision prescribe the adoption of a new belief that is as close as possible to the prior belief, in a process that, even in the standard case, can be described as attempting to minimize surprise. Here we extend the existing model by proposing a measure of surprise, dubbed relative surprise, in which surprise is computed with respect not just to the prior belief, but also to the broader context provided by the new information, using a measure derived from familiar distance notions between truth-value assignments. We characterize the surprise minimization revision operator thus defined using a set of intuitive rationality postulates in the AGM mould, along the way obtaining representation results for other existing revision operators in the literature, such as the Dalal operator and a recently introduced distance-based min-max operator.
Distributing Knowledge into Simple Bases
Mar 31, 2016
Abstract:Understanding the behavior of belief change operators for fragments of classical logic has received increasing interest over the last years. Results in this direction are mainly concerned with adapting representation theorems. However, fragment-driven belief change also leads to novel research questions. In this paper we propose the concept of belief distribution, which can be understood as the reverse task of merging. More specifically, we are interested in the following question: given an arbitrary knowledge base $K$ and some merging operator $\Delta$, can we find a profile $E$ and a constraint $\mu$, both from a given fragment of classical logic, such that $\Delta_\mu(E)$ yields a result equivalent to $K$? In other words, we are interested in seeing if $K$ can be distributed into knowledge bases of simpler structure, such that the task of merging allows for a reconstruction of the original knowledge. Our initial results show that merging based on drastic distance allows for an easy distribution of knowledge, while the power of distribution for operators based on Hamming distance relies heavily on the fragment of choice.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge