Surprise Minimization Revision Operators
Paper and Code
Nov 21, 2021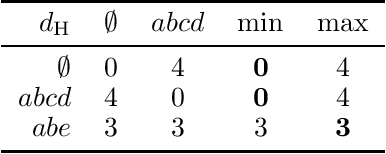
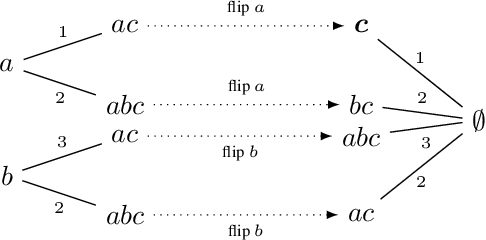

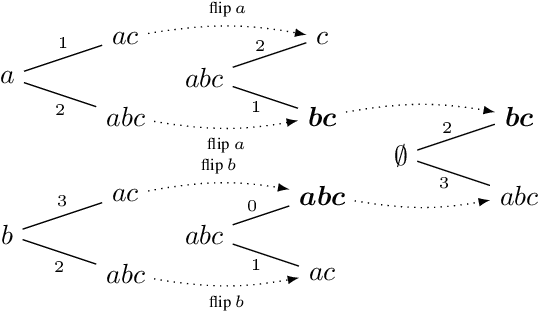
Prominent approaches to belief revision prescribe the adoption of a new belief that is as close as possible to the prior belief, in a process that, even in the standard case, can be described as attempting to minimize surprise. Here we extend the existing model by proposing a measure of surprise, dubbed relative surprise, in which surprise is computed with respect not just to the prior belief, but also to the broader context provided by the new information, using a measure derived from familiar distance notions between truth-value assignments. We characterize the surprise minimization revision operator thus defined using a set of intuitive rationality postulates in the AGM mould, along the way obtaining representation results for other existing revision operators in the literature, such as the Dalal operator and a recently introduced distance-based min-max operator.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge