Fast Multi-Group Gaussian Process Factor Models

Gaussian processes are now commonly used in dimensionality reduction approaches tailored to neuroscience, especially to describe changes in high-dimensional neural activity over time. As recording capabilities expand to include neuronal populations across multiple brain areas, cortical layers, and cell types, interest in extending Gaussian process factor models to characterize multi-population interactions has grown. However, the cubic runtime scaling of current methods with the length of experimental trials and the number of recorded populations (groups) precludes their application to large-scale multi-population recordings. Here, we improve this scaling from cubic to linear in both trial length and group number. We present two approximate approaches to fitting multi-group Gaussian process factor models based on (1) inducing variables and (2) the frequency domain. Empirically, both methods achieved orders of magnitude speed-up with minimal impact on statistical performance, in simulation and on neural recordings of hundreds of neurons across three brain areas. The frequency domain approach, in particular, consistently provided the greatest runtime benefits with the fewest trade-offs in statistical performance. We further characterize the estimation biases introduced by the frequency domain approach and demonstrate effective strategies to mitigate them. This work enables a powerful class of analysis techniques to keep pace with the growing scale of multi-population recordings, opening new avenues for exploring brain function.

Texture Interpolation for Probing Visual Perception

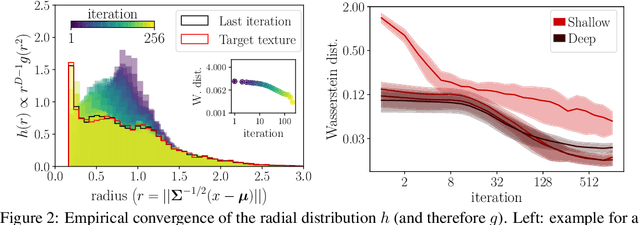
Texture synthesis models are important to understand visual processing. In particular, statistical approaches based on neurally relevant features have been instrumental to understanding aspects of visual perception and of neural coding. New deep learning-based approaches further improve the quality of synthetic textures. Yet, it is still unclear why deep texture synthesis performs so well, and applications of this new framework to probe visual perception are scarce. Here, we show that distributions of deep convolutional neural network (CNN) activations of a texture are well described by elliptical distributions and therefore, following optimal transport theory, constraining their mean and covariance is sufficient to generate new texture samples. Then, we propose the natural geodesics (i.e. the shortest path between two points) arising with the optimal transport metric to interpolate between arbitrary textures. The comparison to alternative interpolation methods suggests that ours matches more closely the geometry of texture perception, and is better suited to study its statistical nature. We demonstrate our method by measuring the perceptual scale associated to the interpolation parameter in human observers, and the neural sensitivity of different areas of visual cortex in macaque monkeys.