Leveraging Large Language Models to Generate Answer Set Programs

Large language models (LLMs), such as GPT-3 and GPT-4, have demonstrated exceptional performance in various natural language processing tasks and have shown the ability to solve certain reasoning problems. However, their reasoning capabilities are limited and relatively shallow, despite the application of various prompting techniques. In contrast, formal logic is adept at handling complex reasoning, but translating natural language descriptions into formal logic is a challenging task that non-experts struggle with. This paper proposes a neuro-symbolic method that combines the strengths of large language models and answer set programming. Specifically, we employ an LLM to transform natural language descriptions of logic puzzles into answer set programs. We carefully design prompts for an LLM to convert natural language descriptions into answer set programs in a step by step manner. Surprisingly, with just a few in-context learning examples, LLMs can generate reasonably complex answer set programs. The majority of errors made are relatively simple and can be easily corrected by humans, thus enabling LLMs to effectively assist in the creation of answer set programs.

NeurASP: Embracing Neural Networks into Answer Set Programming

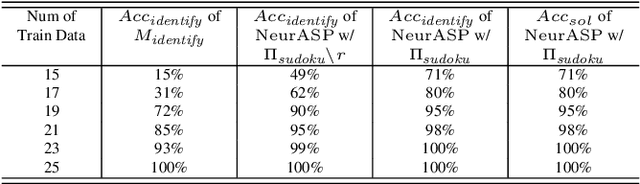
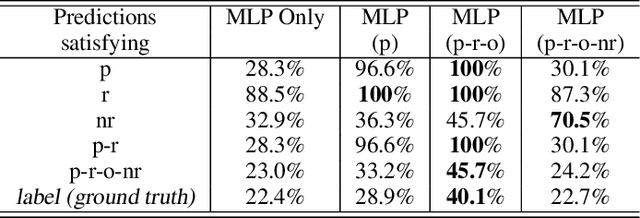
We present NeurASP, a simple extension of answer set programs by embracing neural networks. By treating the neural network output as the probability distribution over atomic facts in answer set programs, NeurASP provides a simple and effective way to integrate sub-symbolic and symbolic computation. We demonstrate how NeurASP can make use of a pre-trained neural network in symbolic computation and how it can improve the neural network's perception result by applying symbolic reasoning in answer set programming. Also, NeurASP can be used to train a neural network better by training with ASP rules so that a neural network not only learns from implicit correlations from the data but also from the explicit complex semantic constraints expressed by the rules.

Coupling Large Language Models with Logic Programming for Robust and General Reasoning from Text

While large language models (LLMs), such as GPT-3, appear to be robust and general, their reasoning ability is not at a level to compete with the best models trained for specific natural language reasoning problems. In this study, we observe that a large language model can serve as a highly effective few-shot semantic parser. It can convert natural language sentences into a logical form that serves as input for answer set programs, a logic-based declarative knowledge representation formalism. The combination results in a robust and general system that can handle multiple question-answering tasks without requiring retraining for each new task. It only needs a few examples to guide the LLM's adaptation to a specific task, along with reusable ASP knowledge modules that can be applied to multiple tasks. We demonstrate that this method achieves state-of-the-art performance on several NLP benchmarks, including bAbI, StepGame, CLUTRR, and gSCAN. Additionally, it successfully tackles robot planning tasks that an LLM alone fails to solve.

Learning to Solve Constraint Satisfaction Problems with Recurrent Transformer

Constraint satisfaction problems (CSPs) are about finding values of variables that satisfy the given constraints. We show that Transformer extended with recurrence is a viable approach to learning to solve CSPs in an end-to-end manner, having clear advantages over state-of-the-art methods such as Graph Neural Networks, SATNet, and some neuro-symbolic models. With the ability of Transformer to handle visual input, the proposed Recurrent Transformer can straightforwardly be applied to visual constraint reasoning problems while successfully addressing the symbol grounding problem. We also show how to leverage deductive knowledge of discrete constraints in the Transformer's inductive learning to achieve sample-efficient learning and semi-supervised learning for CSPs.