Aaditya K. Ramdas
Top-label calibration
Jul 18, 2021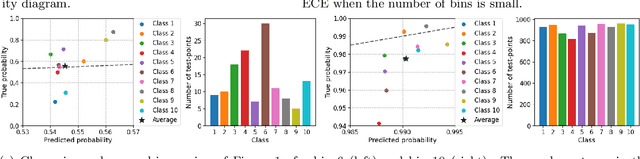
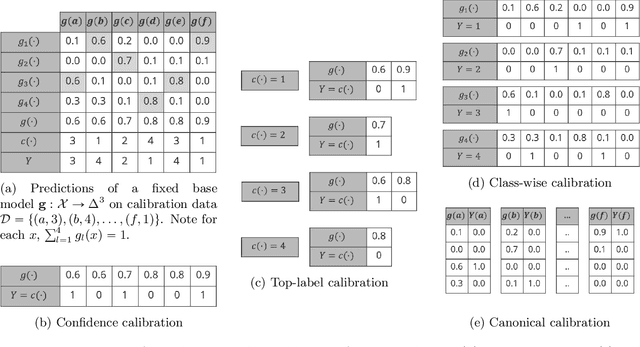

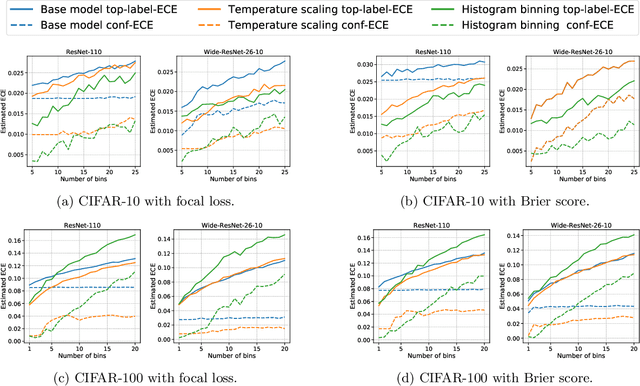
Abstract:We study the problem of post-hoc calibration for multiclass classification, with an emphasis on histogram binning. Multiple works have focused on calibration with respect to the confidence of just the predicted class (or 'top-label'). We find that the popular notion of confidence calibration [Guo et al., 2017] is not sufficiently strong -- there exist predictors that are not calibrated in any meaningful way but are perfectly confidence calibrated. We propose a closely related (but subtly different) notion, top-label calibration, that accurately captures the intuition and simplicity of confidence calibration, but addresses its drawbacks. We formalize a histogram binning (HB) algorithm that reduces top-label multiclass calibration to the binary case, prove that it has clean theoretical guarantees without distributional assumptions, and perform a methodical study of its practical performance. Some prediction tasks require stricter notions of multiclass calibration such as class-wise or canonical calibration. We formalize appropriate HB algorithms corresponding to each of these goals. In experiments with deep neural nets, we find that our principled versions of HB are often better than temperature scaling, for both top-label and class-wise calibration. Code for this work will be made publicly available at https://github.com/aigen/df-posthoc-calibration.
Distribution-free calibration guarantees for histogram binning without sample splitting
May 10, 2021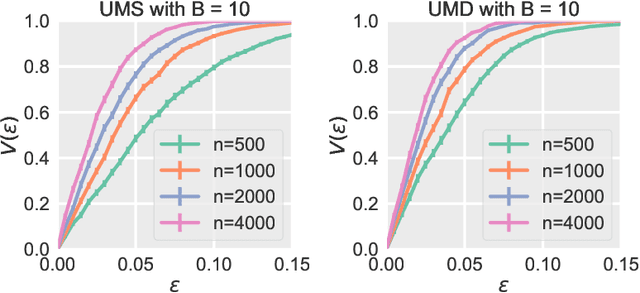
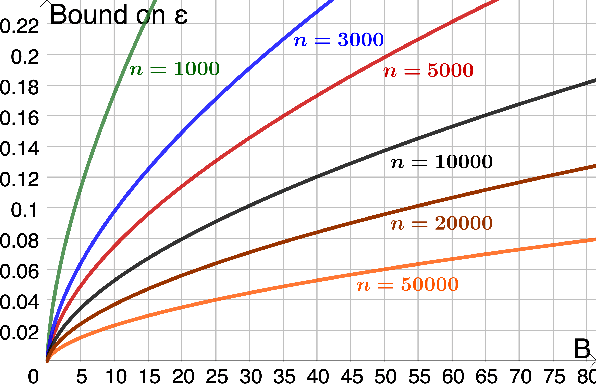
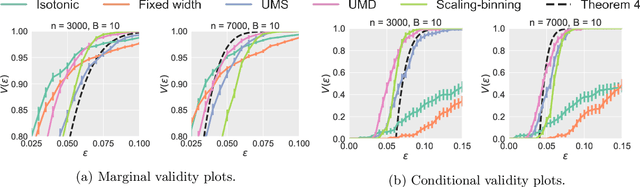
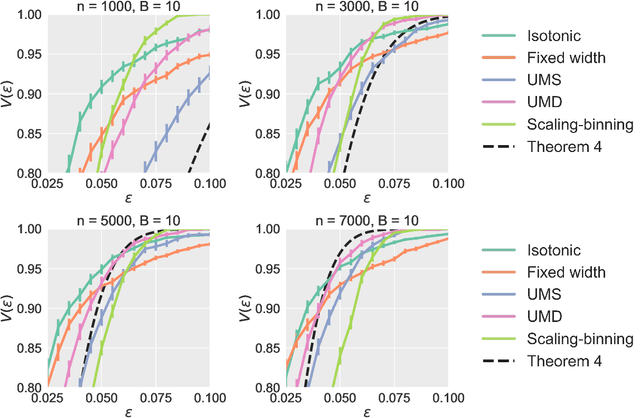
Abstract:We prove calibration guarantees for the popular histogram binning (also called uniform-mass binning) method of Zadrozny and Elkan [2001]. Histogram binning has displayed strong practical performance, but theoretical guarantees have only been shown for sample split versions that avoid 'double dipping' the data. We demonstrate that the statistical cost of sample splitting is practically significant on a credit default dataset. We then prove calibration guarantees for the original method that double dips the data, using a certain Markov property of order statistics. Based on our results, we make practical recommendations for choosing the number of bins in histogram binning. In our illustrative simulations, we propose a new tool for assessing calibration -- validity plots -- which provide more information than an ECE estimate.
Nested Conformal Prediction and the Generalized Jackknife+
Oct 23, 2019
Abstract:We provide an alternate unified framework for conformal prediction, which is a framework to provide assumption-free prediction intervals. Instead of beginning by choosing a conformity score, our framework starts with a sequence of nested sets $\{\mathcal{F}_t(x)\}_{t\in\mathcal{T}}$ for some ordered set $\mathcal{T}$ that specifies all potential prediction sets. We show that most proposed conformity scores in the literature, including several based on quantiles, straightforwardly result in nested families. Then, we argue that what conformal prediction does is find a mapping $\alpha \mapsto t(\alpha)$, meaning that it calibrates or rescales $\mathcal{T}$ to $[0,1]$. Nestedness is a natural and intuitive requirement because the optimal prediction sets (eg: level sets of conditional densities) are also nested, but we also formally prove that nested sets are universal, meaning that any conformal prediction method can be represented in our framework. Finally, to demonstrate its utility, we show how to develop the full conformal, split conformal, cross-conformal and the recent jackknife+ methods within our nested framework, thus immediately generalizing the latter two classes of methods to new settings. Specifically, we prove the validity of the leave-one-out, $K$-fold, subsampling and bootstrap variants of the latter two methods for any nested family.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge