GausSetExpander: A Simple Approach for Entity Set Expansion

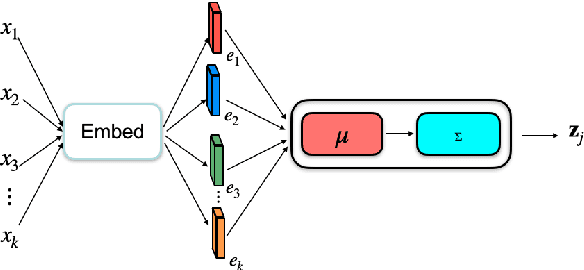
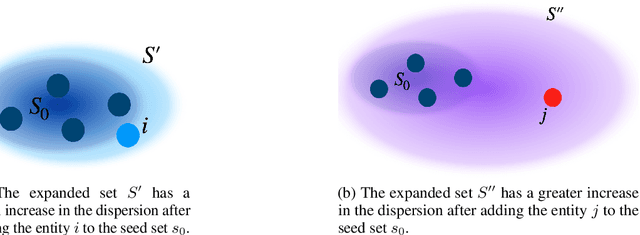
Entity Set Expansion is an important NLP task that aims at expanding a small set of entities into a larger one with items from a large pool of candidates. In this paper, we propose GausSetExpander, an unsupervised approach based on optimal transport techniques. We propose to re-frame the problem as choosing the entity that best completes the seed set. For this, we interpret a set as an elliptical distribution with a centroid which represents the mean and a spread that is represented by the scale parameter. The best entity is the one that increases the spread of the set the least. We demonstrate the validity of our approach by comparing to state-of-the art approaches.

Elliptical Ordinal Embedding

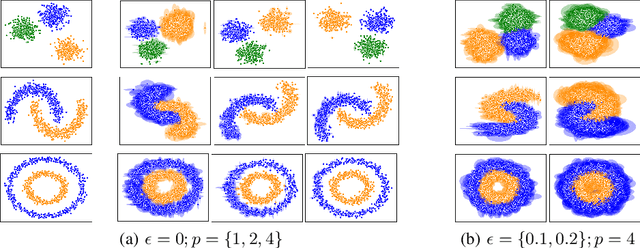
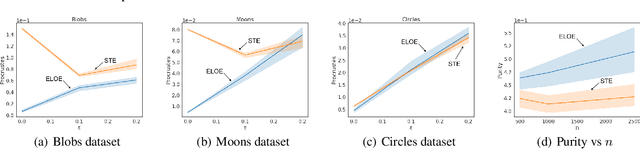
Ordinal embedding aims at finding a low dimensional representation of objects from a set of constraints of the form "item $j$ is closer to item $i$ than item $k$". Typically, each object is mapped onto a point vector in a low dimensional metric space. We argue that mapping to a density instead of a point vector provides some interesting advantages, including an inherent reflection of the uncertainty about the representation itself and its relative location in the space. Indeed, in this paper, we propose to embed each object as a Gaussian distribution. We investigate the ability of these embeddings to capture the underlying structure of the data while satisfying the constraints, and explore properties of the representation. Experiments on synthetic and real-world datasets showcase the advantages of our approach. In addition, we illustrate the merit of modelling uncertainty, which enriches the visual perception of the mapped objects in the space.