Elliptical Ordinal Embedding
Paper and Code
May 25, 2021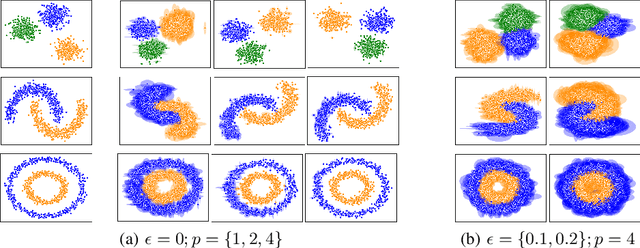

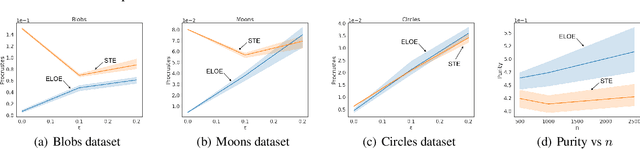
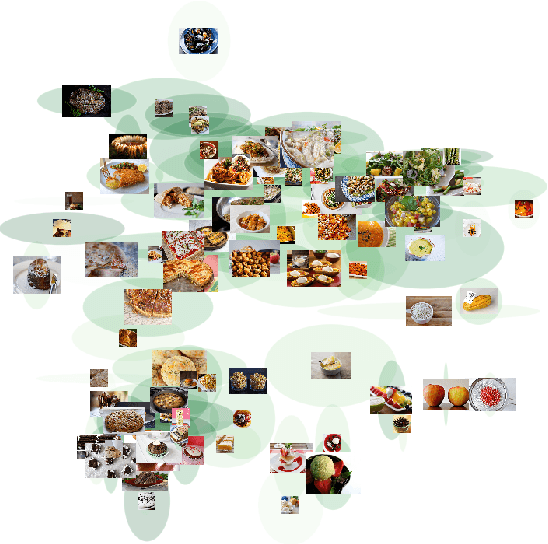
Ordinal embedding aims at finding a low dimensional representation of objects from a set of constraints of the form "item $j$ is closer to item $i$ than item $k$". Typically, each object is mapped onto a point vector in a low dimensional metric space. We argue that mapping to a density instead of a point vector provides some interesting advantages, including an inherent reflection of the uncertainty about the representation itself and its relative location in the space. Indeed, in this paper, we propose to embed each object as a Gaussian distribution. We investigate the ability of these embeddings to capture the underlying structure of the data while satisfying the constraints, and explore properties of the representation. Experiments on synthetic and real-world datasets showcase the advantages of our approach. In addition, we illustrate the merit of modelling uncertainty, which enriches the visual perception of the mapped objects in the space.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge