A Kim Tolbert
MEM_GE: a new maximum entropy method for image reconstruction from solar X-ray visibilities
Feb 18, 2020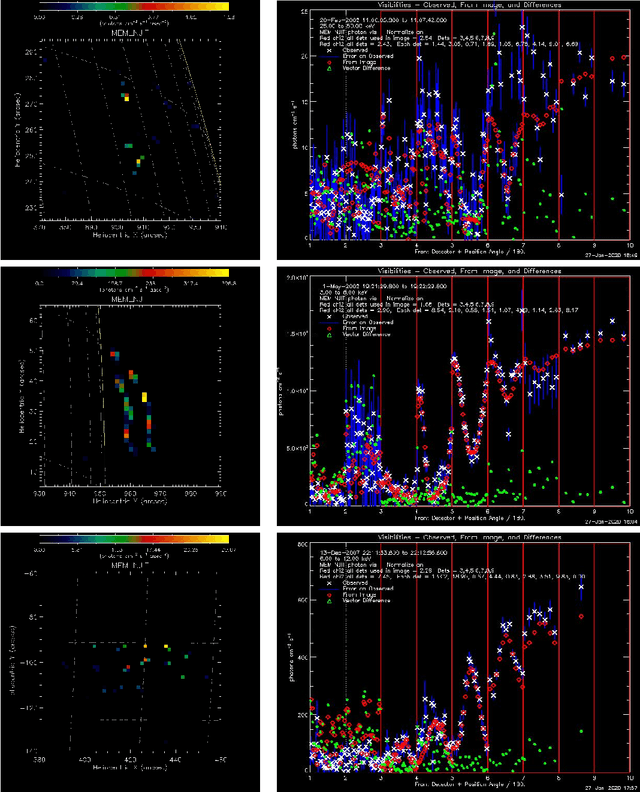
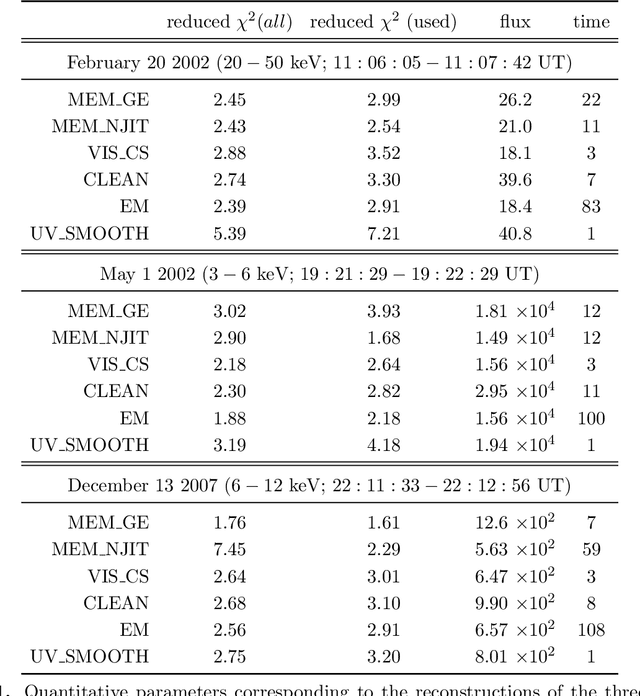

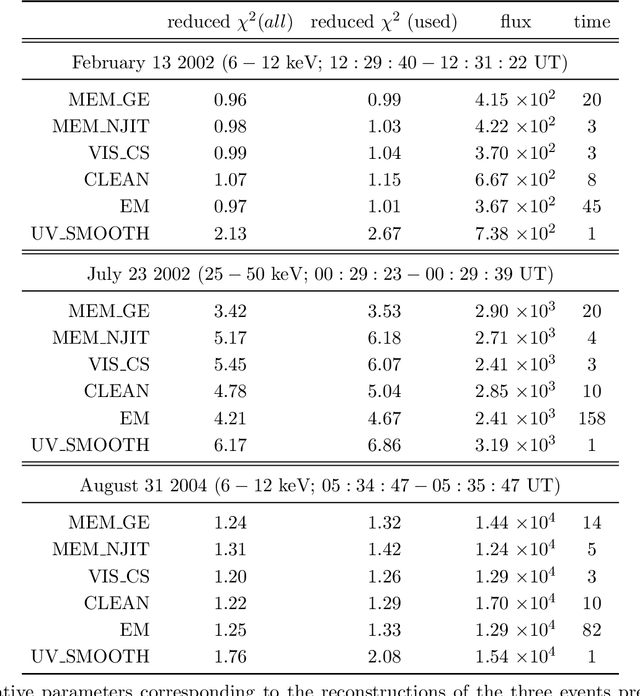
Abstract:Maximum Entropy is an image reconstruction method conceived to image a sparsely occupied field of view and therefore particularly appropriate to achieve super-resolution effects. Although widely used in image deconvolution, this method has been formulated in radio astronomy for the analysis of observations in the spatial frequency domain, and an Interactive Data Language (IDL) code has been implemented for image reconstruction from solar X-ray Fourier data. However, this code relies on a non-convex formulation of the constrained optimization problem addressed by the Maximum Entropy approach and this sometimes results in unreliable reconstructions characterized by unphysical shrinking effects. This paper introduces a new approach to Maximum Entropy based on the constrained minimization of a convex functional. In the case of observations recorded by the Reuven Ramaty High Energy Solar Spectroscopic Imager (RHESSI), the resulting code provides the same super-resolution effects of the previous algorithm, while working properly also when that code produces unphysical reconstructions. Results are also provided of testing the algorithm with synthetic data simulating observations of the Spectrometer/Telescope for Imaging X-rays (STIX) in Solar Orbiter. The new code is available in the {\em{HESSI}} folder of the Solar SoftWare (SSW)tree.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge