Composition of Relational Features with an Application to Explaining Black-Box Predictors

Relational machine learning programs like those developed in Inductive Logic Programming (ILP) offer several advantages: (1) The ability to model complex relationships amongst data instances; (2) The use of domain-specific relations during model construction; and (3) The models constructed are human-readable, which is often one step closer to being human-understandable. However, these ILP-like methods have not been able to capitalise fully on the rapid hardware, software and algorithmic developments fuelling current developments in deep neural networks. In this paper, we treat relational features as functions and use the notion of generalised composition of functions to derive complex functions from simpler ones. We formulate the notion of a set of $\text{M}$-simple features in a mode language $\text{M}$ and identify two composition operators ($\rho_1$ and $\rho_2$) from which all possible complex features can be derived. We use these results to implement a form of "explainable neural network" called Compositional Relational Machines, or CRMs, which are labelled directed-acyclic graphs. The vertex-label for any vertex $j$ in the CRM contains a feature-function $f_j$ and a continuous activation function $g_j$. If $j$ is a "non-input" vertex, then $f_j$ is the composition of features associated with vertices in the direct predecessors of $j$. Our focus is on CRMs in which input vertices (those without any direct predecessors) all have $\text{M}$-simple features in their vertex-labels. We provide a randomised procedure for constructing and learning such CRMs. Using a notion of explanations based on the compositional structure of features in a CRM, we provide empirical evidence on synthetic data of the ability to identify appropriate explanations; and demonstrate the use of CRMs as 'explanation machines' for black-box models that do not provide explanations for their predictions.

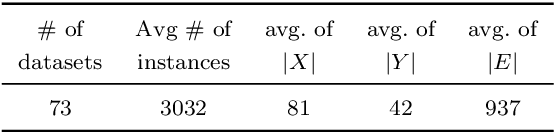
Inclusion of Domain-Knowledge into GNNs using Mode-Directed Inverse Entailment

We present a general technique for constructing Graph Neural Networks (GNNs) capable of using multi-relational domain knowledge. The technique is based on mode-directed inverse entailment (MDIE) developed in Inductive Logic Programming (ILP). Given a data instance $e$ and background knowledge $B$, MDIE identifies a most-specific logical formula $\bot_B(e)$ that contains all the relational information in $B$ that is related to $e$. We transform $\bot_B(e)$ into a corresponding "bottom-graph" that can be processed for use by standard GNN implementations. This transformation allows a principled way of incorporating generic background knowledge into GNNs: we use the term `BotGNN' for this form of graph neural networks. For several GNN variants, using real-world datasets with substantial background knowledge, we show that BotGNNs perform significantly better than both GNNs without background knowledge and a recently proposed simplified technique for including domain knowledge into GNNs. We also provide experimental evidence comparing BotGNNs favourably to multi-layer perceptrons (MLPs) that use features representing a "propositionalised" form of the background knowledge; and BotGNNs to a standard ILP based on the use of most-specific clauses. Taken together, these results point to BotGNNs as capable of combining the computational efficacy of GNNs with the representational versatility of ILP.