Identification of Cancer Patient Subgroups via Smoothed Shortest Path Graph Kernel

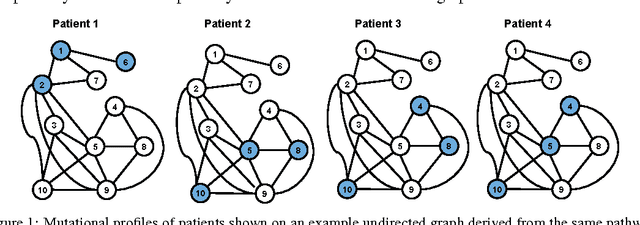
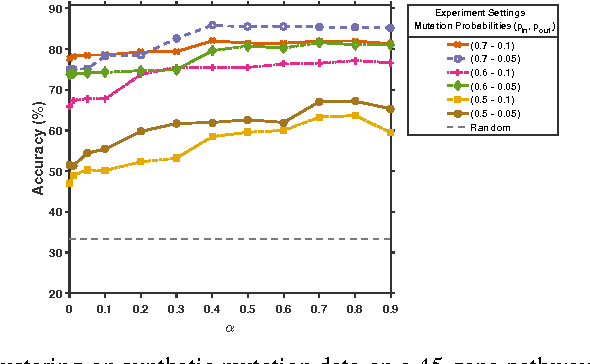
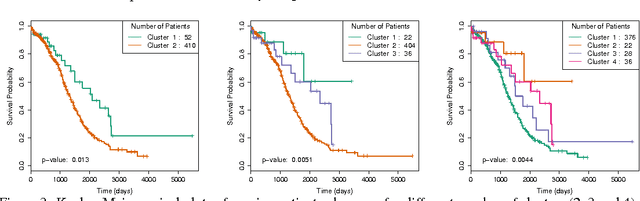
Characterizing patient somatic mutations through next-generation sequencing technologies opens up possibilities for refining cancer subtypes. However, catalogues of mutations reveal that only a small fraction of the genes are altered frequently in patients. On the other hand different genomic alterations may perturb the same pathways. We propose a novel clustering procedure that quantifies the similarities of patients from their mutational profile on pathways via a novel graph kernel. We represent each KEGG pathway as an undirected graph. For each patient the vertex labels are assigned based on her altered genes. Smoothed shortest path graph kernel (smSPK) evaluates each pair of patients by comparing their vertex labeled pathway graphs. Our clustering procedure involves two steps: the smSPK kernel matrix derived for each pathway are input to kernel k-means algorithm and each pathway is evaluated individually. In the next step, only those pathways that are successful are combined in to a single kernel input to kernel k-means to stratify patients. Evaluating the procedure on simulated data showed that smSPK clusters patients up to 88\% accuracy. Finally to identify ovarian cancer patient subgroups, we apply our methodology to the cancer genome atlas ovarian data that involves 481 patients. The identified subgroups are evaluated through survival analysis. Grouping patients into four clusters results with patients groups that are significantly different in their survival times ($p$-value $\le 0.005$).

ALEVS: Active Learning by Statistical Leverage Sampling

Active learning aims to obtain a classifier of high accuracy by using fewer label requests in comparison to passive learning by selecting effective queries. Many active learning methods have been developed in the past two decades, which sample queries based on informativeness or representativeness of unlabeled data points. In this work, we explore a novel querying criterion based on statistical leverage scores. The statistical leverage scores of a row in a matrix are the squared row-norms of the matrix containing its (top) left singular vectors and is a measure of influence of the row on the matrix. Leverage scores have been used for detecting high influential points in regression diagnostics and have been recently shown to be useful for data analysis and randomized low-rank matrix approximation algorithms. We explore how sampling data instances with high statistical leverage scores perform in active learning. Our empirical comparison on several binary classification datasets indicate that querying high leverage points is an effective strategy.