Your Contrastive Learning Is Secretly Doing Stochastic Neighbor Embedding

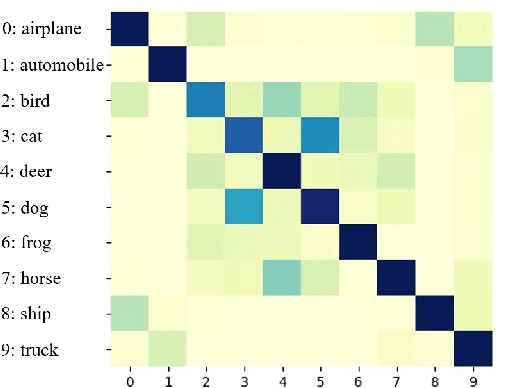
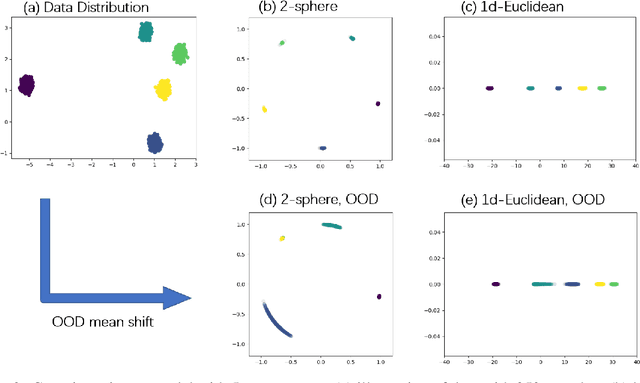
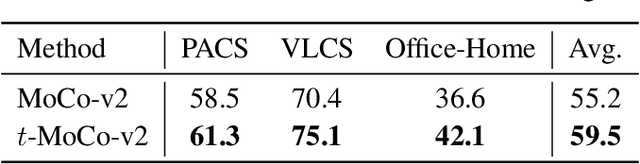
Contrastive learning, especially Self-Supervised Contrastive Learning (SSCL), has achieved great success in extracting powerful features from unlabeled data, enabling comparable performance to the supervised counterpart. In this work, we contribute to the theoretical understanding of SSCL and uncover its connection to the classic data visualization method, Stochastic Neighbor Embedding (SNE). In the perspective of SNE, whose goal is matching pairwise distance, SSCL can be viewed as a special case with the input space pairwise distance specified by constructed "positive" pairs from data augmentation. The established correspondence facilitates deeper theoretical understandings of learned features of SSCL, as well as methodological guidelines for practical improvement. Specifically, through the lens of SNE, not only can we re-derive the alignment and uniformity principle, but also provide novel analysis on domain-agnostic augmentations and implicit bias. To illustrate the practical advantage, we demonstrate that the modifications from SNE to $t$-SNE can also be adopted in the SSCL setting, achieving significant improvement in both in-distribution and out-of-distribution generalization.