You KAN Do It in a Single Shot: Plug-and-Play Methods with Single-Instance Priors
Paper and Code
Dec 09, 2024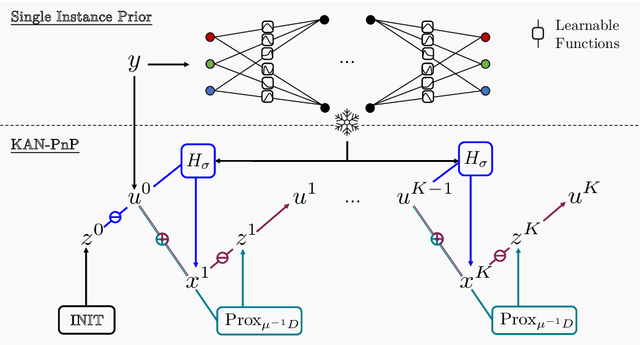
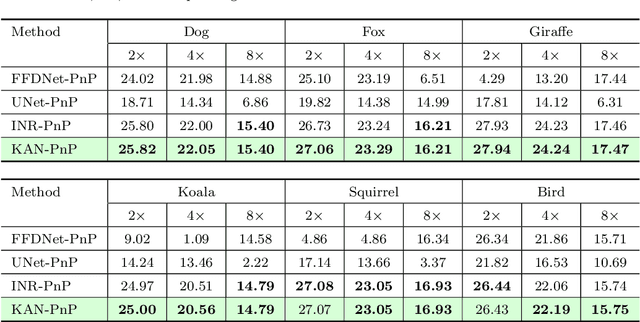

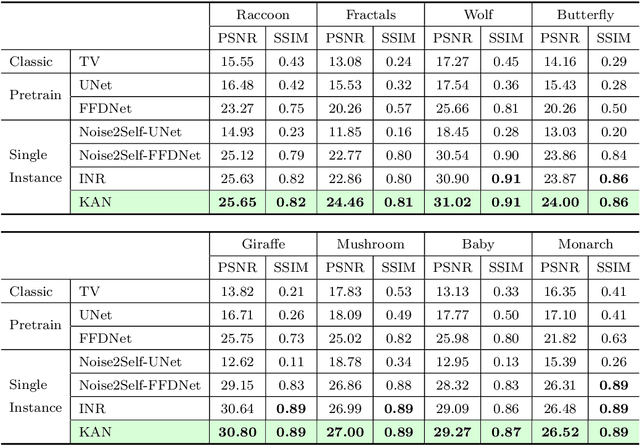
The use of Plug-and-Play (PnP) methods has become a central approach for solving inverse problems, with denoisers serving as regularising priors that guide optimisation towards a clean solution. In this work, we introduce KAN-PnP, an optimisation framework that incorporates Kolmogorov-Arnold Networks (KANs) as denoisers within the Plug-and-Play (PnP) paradigm. KAN-PnP is specifically designed to solve inverse problems with single-instance priors, where only a single noisy observation is available, eliminating the need for large datasets typically required by traditional denoising methods. We show that KANs, based on the Kolmogorov-Arnold representation theorem, serve effectively as priors in such settings, providing a robust approach to denoising. We prove that the KAN denoiser is Lipschitz continuous, ensuring stability and convergence in optimisation algorithms like PnP-ADMM, even in the context of single-shot learning. Additionally, we provide theoretical guarantees for KAN-PnP, demonstrating its convergence under key conditions: the convexity of the data fidelity term, Lipschitz continuity of the denoiser, and boundedness of the regularisation functional. These conditions are crucial for stable and reliable optimisation. Our experimental results show, on super-resolution and joint optimisation, that KAN-PnP outperforms exiting methods, delivering superior performance in single-shot learning with minimal data. The method exhibits strong convergence properties, achieving high accuracy with fewer iterations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge