Xi-Learning: Successor Feature Transfer Learning for General Reward Functions

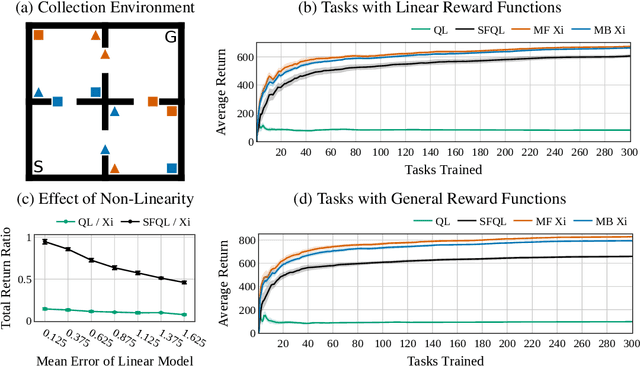
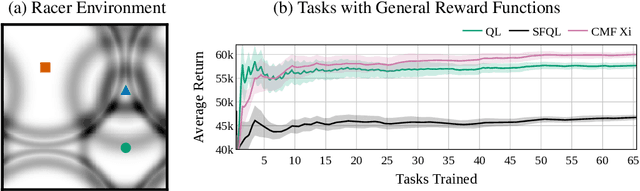
Transfer in Reinforcement Learning aims to improve learning performance on target tasks using knowledge from experienced source tasks. Successor features (SF) are a prominent transfer mechanism in domains where the reward function changes between tasks. They reevaluate the expected return of previously learned policies in a new target task and to transfer their knowledge. A limiting factor of the SF framework is its assumption that rewards linearly decompose into successor features and a reward weight vector. We propose a novel SF mechanism, $\xi$-learning, based on learning the cumulative discounted probability of successor features. Crucially, $\xi$-learning allows to reevaluate the expected return of policies for general reward functions. We introduce two $\xi$-learning variations, prove its convergence, and provide a guarantee on its transfer performance. Experimental evaluations based on $\xi$-learning with function approximation demonstrate the prominent advantage of $\xi$-learning over available mechanisms not only for general reward functions, but also in the case of linearly decomposable reward functions.