Why MDAC? A Multi-domain Activation Function

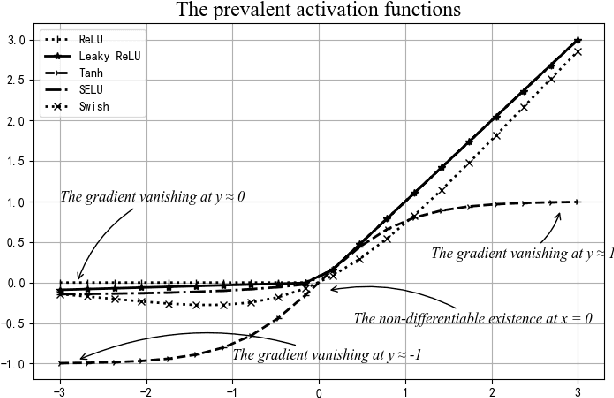
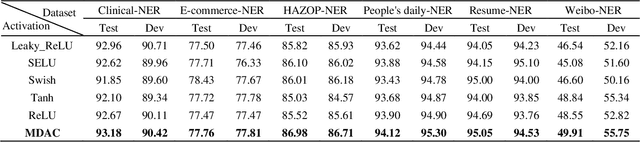
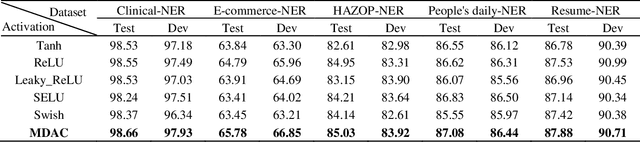
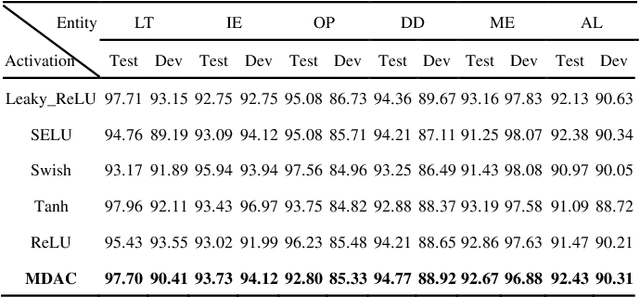
In this study, a novel, general and ingenious activation function termed MDAC is proposed to surmount the troubles of gradient vanishing and non-differentiable existence. MDAC approximately inherits the properties of exponential activation function (such as Tanh family) and piecewise linear activation function (such as ReLU family). Specifically, in the positive region, the adaptive linear structure is designed to respond to various domain distributions. In the negative region, the combination of exponent and linearity is considered to conquer the obstacle of gradient vanishing. Furthermore, the non-differentiable existence is eliminated by smooth approximation. Experiments show that MDAC improves performance on both classical models and pre-training optimization models in six domain datasets by simply changing the activation function, which indicates MDAC's effectiveness and pro-gressiveness. MDAC is superior to other prevalent activation functions in robustness and generalization, and can reflect excellent activation performance in multiple domains.