Why Does MAML Outperform ERM? An Optimization Perspective

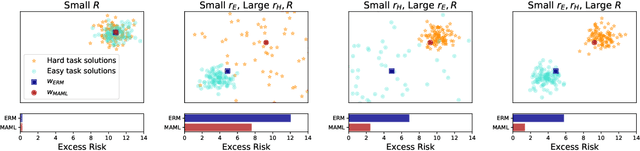
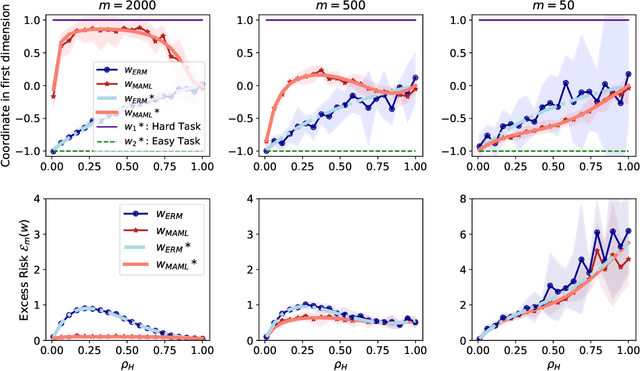
Model-Agnostic Meta-Learning (MAML) has demonstrated widespread success in training models that can quickly adapt to new tasks via one or few stochastic gradient descent steps. However, the MAML objective is significantly more difficult to optimize compared to standard Empirical Risk Minimization (ERM), and little is understood about how much MAML improves over ERM in terms of the fast adaptability of their solutions in various scenarios. We analytically address this issue in a linear regression setting consisting of a mixture of easy and hard tasks, where hardness is determined by the number of gradient steps required to solve the task. Specifically, we prove that for $\Omega(d_{\text{eff}})$ labelled test samples (for gradient-based fine-tuning) where $d_{\text{eff}}$ is the effective dimension of the problem, in order for MAML to achieve substantial gain over ERM, the optimal solutions of the hard tasks must be closely packed together with the center far from the center of the easy task optimal solutions. We show that these insights also apply in a low-dimensional feature space when both MAML and ERM learn a representation of the tasks, which reduces the effective problem dimension. Further, our few-shot image classification experiments suggest that our results generalize beyond linear regression.