Who Spoke What? A Latent Variable Framework for the Joint Decoding of Multiple Speakers and their Keywords
Paper and Code
Apr 29, 2015
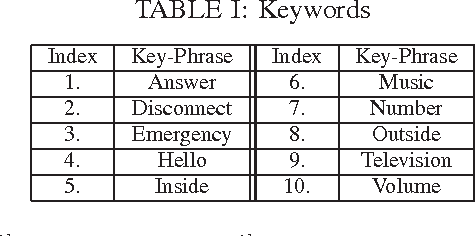
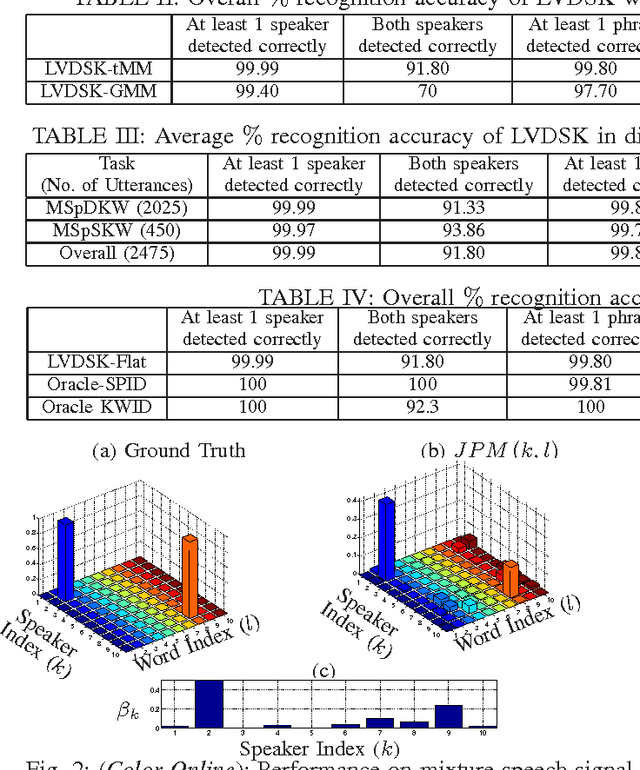
In this paper, we present a latent variable (LV) framework to identify all the speakers and their keywords given a multi-speaker mixture signal. We introduce two separate LVs to denote active speakers and the keywords uttered. The dependency of a spoken keyword on the speaker is modeled through a conditional probability mass function. The distribution of the mixture signal is expressed in terms of the LV mass functions and speaker-specific-keyword models. The proposed framework admits stochastic models, representing the probability density function of the observation vectors given that a particular speaker uttered a specific keyword, as speaker-specific-keyword models. The LV mass functions are estimated in a Maximum Likelihood framework using the Expectation Maximization (EM) algorithm. The active speakers and their keywords are detected as modes of the joint distribution of the two LVs. In mixture signals, containing two speakers uttering the keywords simultaneously, the proposed framework achieves an accuracy of 82% for detecting both the speakers and their respective keywords, using Student's-t mixture models as speaker-specific-keyword models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge