Where You Are Is Who You Are: User Identification by Matching Statistics
Paper and Code
Dec 09, 2015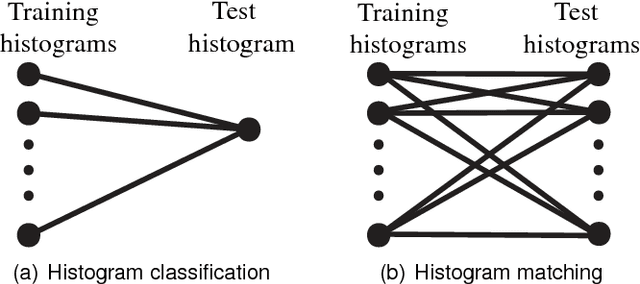
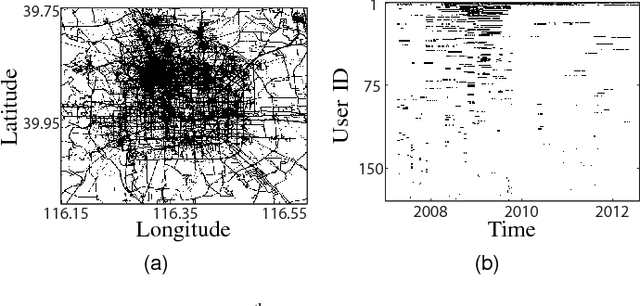
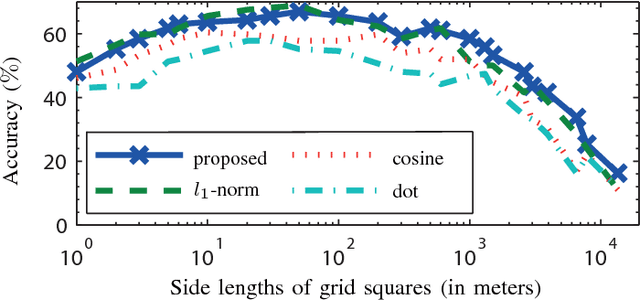
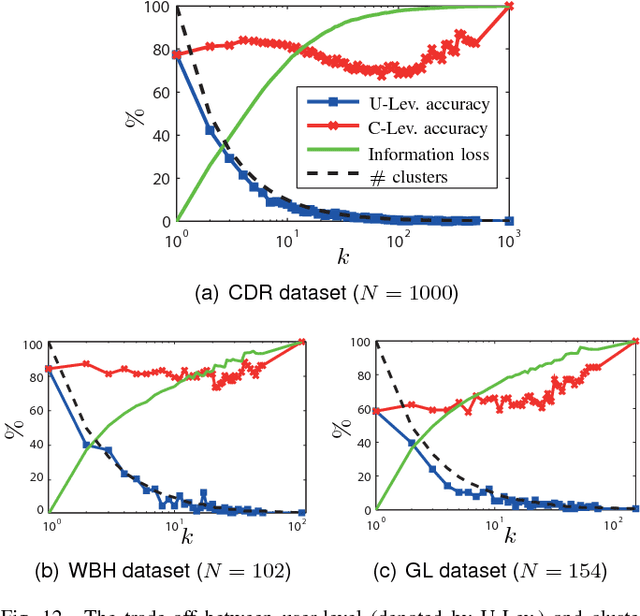
Most users of online services have unique behavioral or usage patterns. These behavioral patterns can be exploited to identify and track users by using only the observed patterns in the behavior. We study the task of identifying users from statistics of their behavioral patterns. Specifically, we focus on the setting in which we are given histograms of users' data collected during two different experiments. We assume that, in the first dataset, the users' identities are anonymized or hidden and that, in the second dataset, their identities are known. We study the task of identifying the users by matching the histograms of their data in the first dataset with the histograms from the second dataset. In recent works, the optimal algorithm for this user identification task is introduced. In this paper, we evaluate the effectiveness of this method on three different types of datasets and in multiple scenarios. Using datasets such as call data records, web browsing histories, and GPS trajectories, we show that a large fraction of users can be easily identified given only histograms of their data; hence these histograms can act as users' fingerprints. We also verify that simultaneous identification of users achieves better performance compared to one-by-one user identification. We show that using the optimal method for identification gives higher identification accuracy than heuristics-based approaches in practical scenarios. The accuracy obtained under this optimal method can thus be used to quantify the maximum level of user identification that is possible in such settings. We show that the key factors affecting the accuracy of the optimal identification algorithm are the duration of the data collection, the number of users in the anonymized dataset, and the resolution of the dataset. We analyze the effectiveness of k-anonymization in resisting user identification attacks on these datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge