What You See May Not Be What You Get: UCB Bandit Algorithms Robust to ε-Contamination
Paper and Code
Oct 12, 2019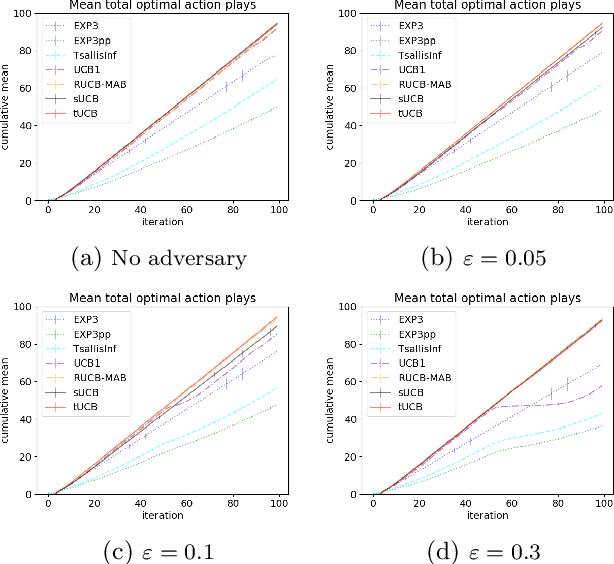
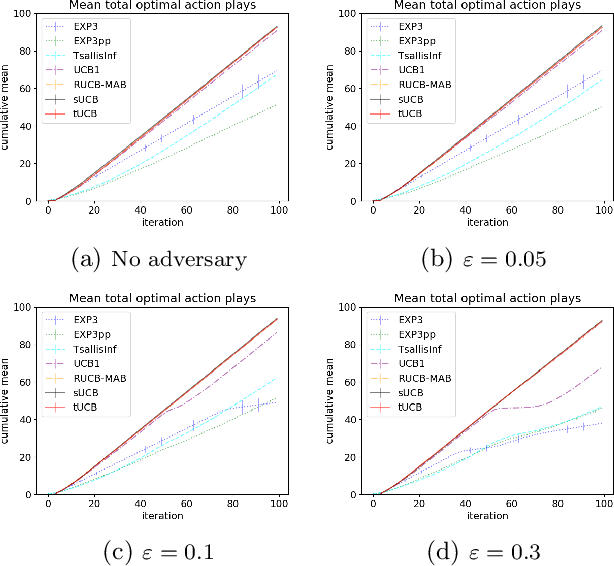
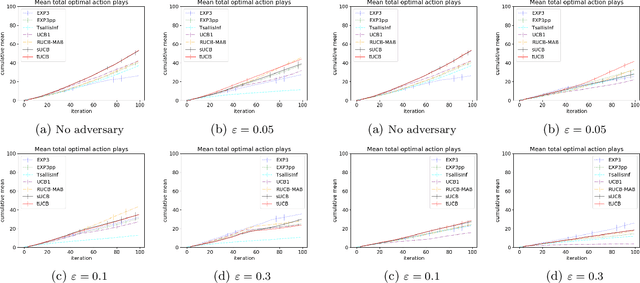
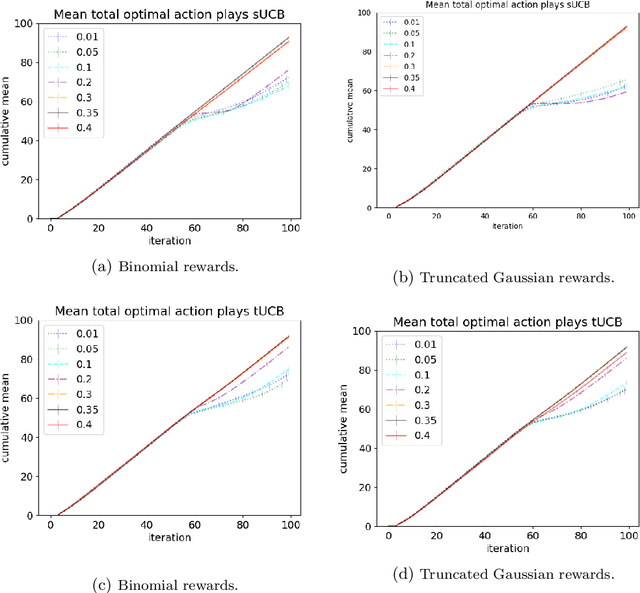
Motivated by applications of bandit algorithms in education, we consider a stochastic multi-armed bandit problem with $\varepsilon$-contaminated rewards. We allow an adversary to arbitrarily give unbounded contaminated rewards with full knowledge of the past and future. We impose only the constraint that at any time $t$ the proportion of contaminated rewards for any action is less than or equal to $\varepsilon$. We derive concentration inequalities for two robust mean estimators for sub-Gaussian distributions in the $\varepsilon$-contamination context. We define the $\varepsilon$-contaminated stochastic bandit problem and use our robust mean estimators to give two variants of a robust Upper Confidence Bound (UCB) algorithm, crUCB. Using regret derived from only the underlying stochastic rewards, both variants of crUCB achieve $\mathcal{O} (\sqrt{KT\log T})$ regret when $\varepsilon$ is small enough. Our simulations are designed to reflect reasonable settings a teacher would experience when implementing a bandit algorithm and thus use a limited horizon. We show that in certain adversarial regimes crUCB not only outperforms algorithms designed for stochastic (UCB1) and adversarial bandits (EXP3) but also those that have "best of both worlds" guarantees (EXP3++ and TsallisInf) even when our constraint on $\varepsilon$ is broken.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge