Weighted Tensor Completion for Time-Series Causal Inference

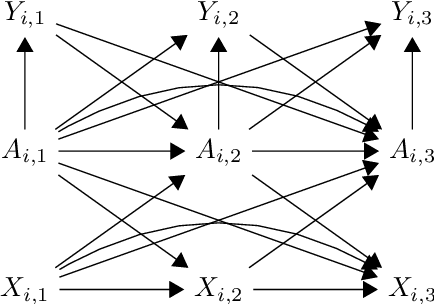
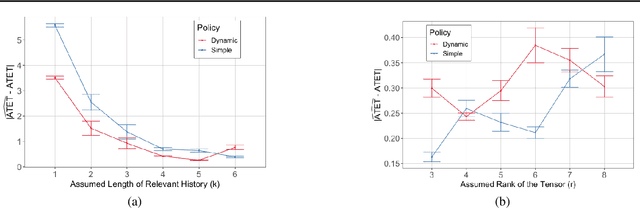
Marginal Structural Models (MSM) {Robins, 2000} are the most popular models for causal inference from time-series observational data. However, they have two main drawbacks: (a) they do not capture subject heterogeneity, and (b) they only consider fixed time intervals and do not scale gracefully with longer intervals. In this work, we propose a new family of MSMs to address these two concerns. We model the potential outcomes as a three-dimensional tensor of low rank, where the three dimensions correspond to the agents, time periods and the set of possible histories. Unlike the traditional MSM, we allow the dimensions of the tensor to increase with the number of agents and time periods. We set up a weighted tensor completion problem as our estimation procedure, and show that the solution to this problem converges to the true model in an appropriate sense. Then we show how to solve the estimation problem, providing conditions under which we can approximately and efficiently solve the estimation problem. Finally, we propose an algorithm based on projected gradient descent, which is easy to implement and evaluate its performance on a simulated dataset.