Weighted Sampling for Combined Model Selection and Hyperparameter Tuning

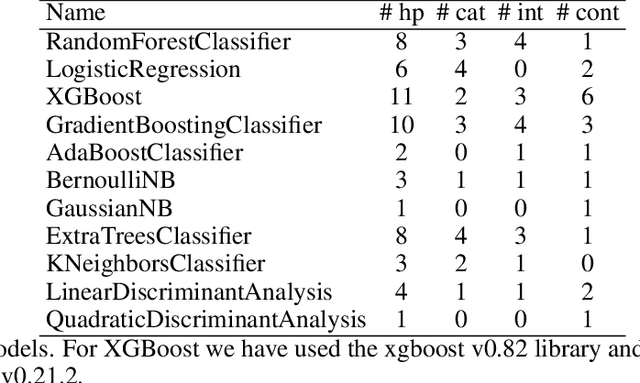
The combined algorithm selection and hyperparameter tuning (CASH) problem is characterized by large hierarchical hyperparameter spaces. Model-free hyperparameter tuning methods can explore such large spaces efficiently since they are highly parallelizable across multiple machines. When no prior knowledge or meta-data exists to boost their performance, these methods commonly sample random configurations following a uniform distribution. In this work, we propose a novel sampling distribution as an alternative to uniform sampling and prove theoretically that it has a better chance of finding the best configuration in a worst-case setting. In order to compare competing methods rigorously in an experimental setting, one must perform statistical hypothesis testing. We show that there is little-to-no agreement in the automated machine learning literature regarding which methods should be used. We contrast this disparity with the methods recommended by the broader statistics literature, and identify the most suitable approach. We then select three popular model-free solutions to CASH and evaluate their performance, with uniform sampling as well as the proposed sampling scheme, across 67 datasets from the OpenML platform. We investigate the trade-off between exploration and exploitation across the three algorithms, and verify empirically that the proposed sampling distribution improves performance in all cases.