Wasserstein Coresets for Lipschitz Costs

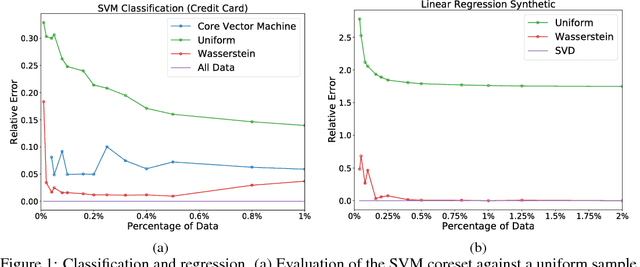
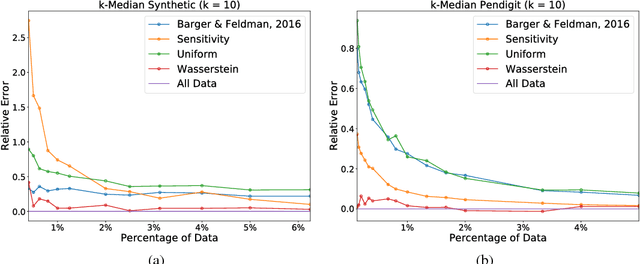
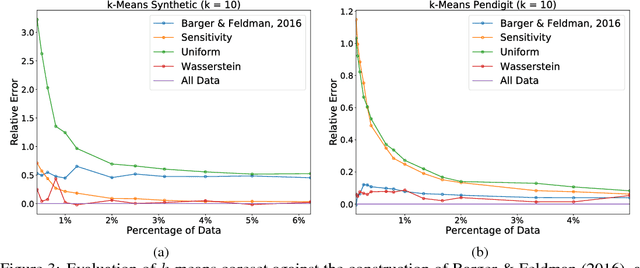
Sparsification is becoming more and more relevant with the proliferation of huge data sets. Coresets are a principled way to construct representative weighted subsets of a data set that have matching performance with the full data set for specific problems. However, coreset language neglects the nature of the underlying data distribution, which is often continuous. In this paper, we address this oversight by introducing a notion of measure coresets that generalizes coreset language to arbitrary probability measures. Our definition reveals a surprising connection to optimal transport theory which we leverage to design a coreset for problems with Lipschitz costs. We validate our construction on support vector machine (SVM) training, k-means clustering, k-median clustering, and linear regression and show that we are competitive with previous coreset constructions.