VPE: Variational Policy Embedding for Transfer Reinforcement Learning
Paper and Code
Sep 14, 2018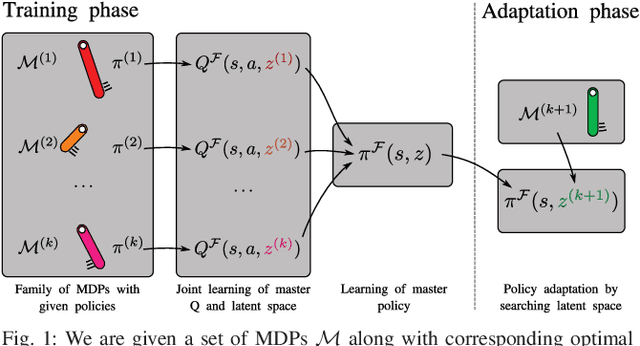

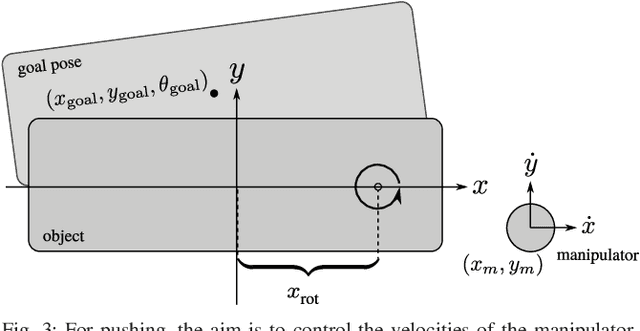

Reinforcement Learning methods are capable of solving complex problems, but resulting policies might perform poorly in environments that are even slightly different. In robotics especially, training and deployment conditions often vary and data collection is expensive, making retraining undesirable. Simulation training allows for feasible training times, but on the other hand suffers from a reality-gap when applied in real-world settings. This raises the need of efficient adaptation of policies acting in new environments. We consider this as a problem of transferring knowledge within a family of similar Markov decision processes. For this purpose we assume that Q-functions are generated by some low-dimensional latent variable. Given such a Q-function, we can find a master policy that can adapt given different values of this latent variable. Our method learns both the generative mapping and an approximate posterior of the latent variables, enabling identification of policies for new tasks by searching only in the latent space, rather than the space of all policies. The low-dimensional space, and master policy found by our method enables policies to quickly adapt to new environments. We demonstrate the method on both a pendulum swing-up task in simulation, and for simulation-to-real transfer on a pushing task.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge