Virtual Node Generation for Node Classification in Sparsely-Labeled Graphs
Paper and Code
Sep 12, 2024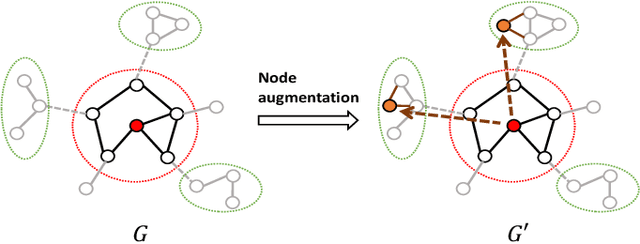
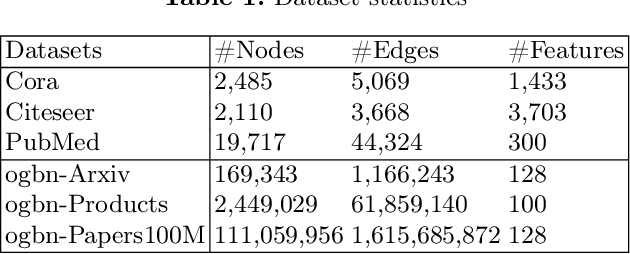
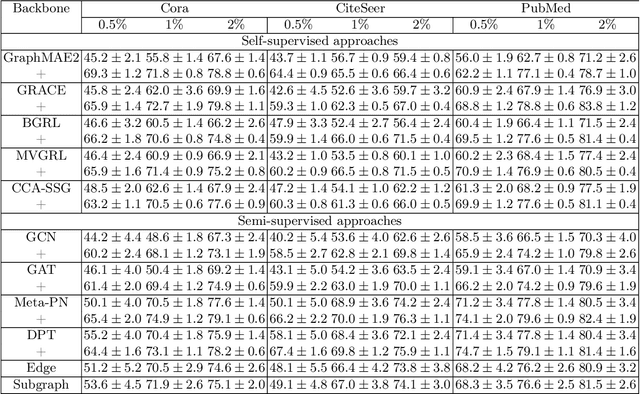
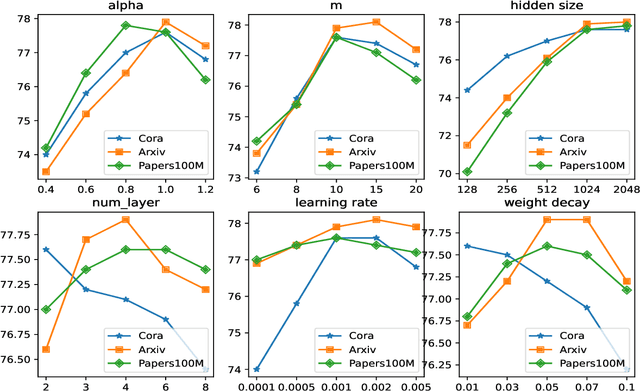
In the broader machine learning literature, data-generation methods demonstrate promising results by generating additional informative training examples via augmenting sparse labels. Such methods are less studied in graphs due to the intricate dependencies among nodes in complex topology structures. This paper presents a novel node generation method that infuses a small set of high-quality synthesized nodes into the graph as additional labeled nodes to optimally expand the propagation of labeled information. By simply infusing additional nodes, the framework is orthogonal to the graph learning and downstream classification techniques, and thus is compatible with most popular graph pre-training (self-supervised learning), semi-supervised learning, and meta-learning methods. The contribution lies in designing the generated node set by solving a novel optimization problem. The optimization places the generated nodes in a manner that: (1) minimizes the classification loss to guarantee training accuracy and (2) maximizes label propagation to low-confidence nodes in the downstream task to ensure high-quality propagation. Theoretically, we show that the above dual optimization maximizes the global confidence of node classification. Our Experiments demonstrate statistically significant performance improvements over 14 baselines on 10 publicly available datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge